TLDR: I'll fill the board and prove that the solution is unique.
First, let's start by:
Looking for corners where T tetrominoes could only be filled in by no more than one unique way.
I'll paint those green:

Let's repeat those steps a few more times, using orange, blue, red and purple, in precisely that order:

Now,
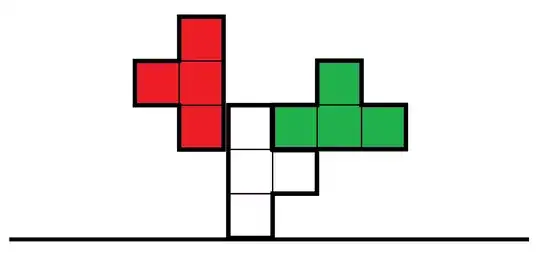
let's focus on the topmost white square.
It can't be filled by a right-looking T tetromino, because this would imply a sequence of two white squares in the left, where one of then couldn't be filled in any way. It also can't be a left-looking or down-looking because this would leave a isolated sole white square. Thus, it must be up-looking (brown):

We can easily fill the topmost white squares by that reasoning. They can't be filled in any other way:

Now, let's look at:
The bottommost white cells, at the right side of a green tetromino.
The white cell at the very right of the green-painted tetromino could only be filled with an up-looking tetromino, or a right-looking one. However the right-looking one would leave a isolated white cell. So it must be filled with an up-looking one (brown again):

And by repatedly filling the remaining squares with the only obvious possibility every time:

Now the problem is divided in two. Let's start with the upper part:
There is more than one way to fill this with tetrominoes. But only one of them respect gravity.
Look at the white spaces right to the light blue tetromino. If you put a right-looking or a down-looking one, it would leave isolated white cells. So the tetromino at this spot must be either up-looking or left-looking. Let's try a left-looking. Under it, we won't have space to put a right-looking or a left-looking tetromino, so we can try a down-looking or a up-looking one:
Down-looking:

Up-looking:

So it must be up-looking:

The rest of the upper part:
Let's start with the bottommost part of the upper white spaces. If you put a right-looking tetromino or an up-looking tetromino, you would leave single white cells hanging around.
What if we put a left-looking one?

So:
It must be down-looking. The remaining cells in the uppermost part can also only be filled in one way respecting gravity:

To the bottom part:
Let's start with the rightmost white cell. An up-looking or left-looking tetromino would leave solitary white cells. So it must be either right-looking or down-looking.
Let's try a right-looking one:

Trying to change the position or flipping the blue tetromino is also hopeless. There is no way to fill both the white cells at the red tetromino's left.
So, using a down-looking and filling the obvious spaces:

And there is only a single way to finish without defying gravity:

DONE!