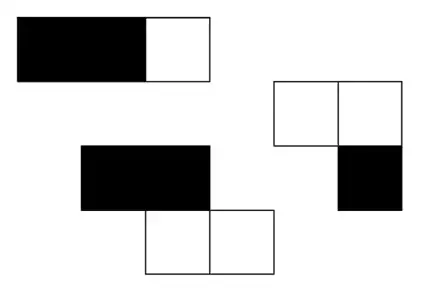
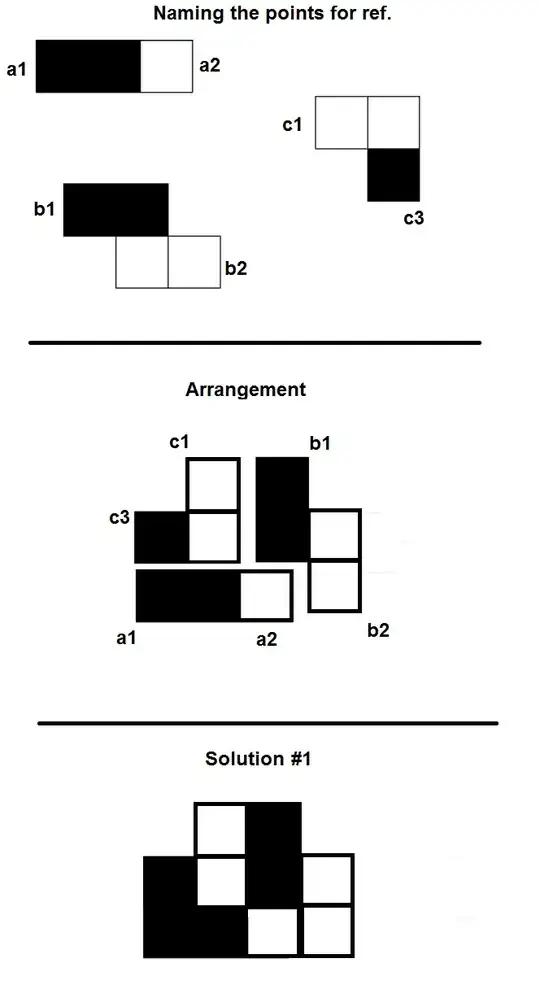
Here are 6 solutions, with instructions for another 77,771.
The seed solution’s shape came from seeking threefold angular symmetry,
for rotational simplicity,
with the hope that one solution can become 77,777
merely by stretching such a configuration.
 
(Good news, stretching worked as hoped.)
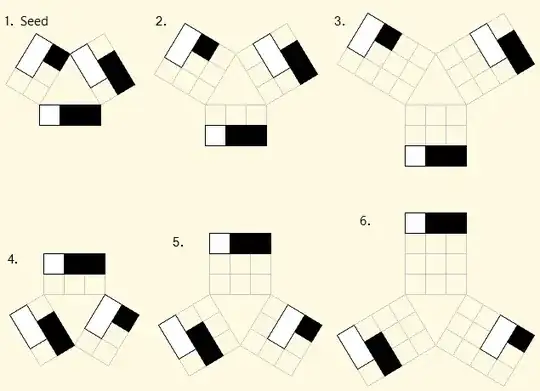
Note that solutions 4− 6 are
similar to solutions 1− 3,
as if the pieces had passed through the center.
Thanks to
elias’s insight
that one solution can become another by rotating the pieces by equal amounts,
solutions 4− 6 can also be derived
from solutions 1− 3
by turning each piece 180° locally
before turning the entire plane 180°.
The seed solution’s details came from discovering
that the pieces could be repeated to produce
equal black and white patterns
shifted relative to each other.

The pieces might as well have their own coordinate-system grids,
at 120° angles to each other.
 
For any of 77,771 further solutions,
just select virtually any coordinate pair
and orientation and place each piece on its own grid,
at those coordinates and with that orientation.
 
Here is a picture of those grids,
with a solution for coordinates (-3.5, 4)
and orientation 90° counter-clockwise and flipped.

Here are those pieces and their grids individually and compared
to their seed positions /orientations.

These coordinate grids could also be extended out of the plane
(violating the puzzle statement)
to produce congruent 3-dimensional color patterns.
That is, each piece could also be
tilted and lifted out of the plane by a common
arbitrary altitudinal angle and arbitrary offset
along with elias’s arbitrary azimuthal angle.