The riddle is impossible to solve with absolute certainty and I can prove it.
I have been spending quite some time on this problem and I honestly don't think it's solvable. I think that the solutions presented here neglect a lot of information which can be logically inferred by the two prisoners with what they already know following perfect logics. If this additional information is accounted for, I honestly don't understand how the problem is solvable.
Unless I am missing something in my framing of the problem (which I will write hereafter), I think that the only reason why the proposed solutions work is because they implicitly assume that the two prisoners follow the same logic presented in the solution, which coincidentally leads to a unique solution deducible by both prisoners. In other words, the reason why the two prisoners can solve the riddle with absolute certainty is not because of pure logics, but because they are unknowingly following a shared strategy by which they are able to exchange useful information to infer each other's number.
I will propose here a perfectly logical and coherent framework by which no solution is possible. The fact that such a possibility exists means that if the any of the two prisoners doesn't follow a strategy, they might in principle follow the logics proposed here, which would in itself make the riddle impossible to solve with pure logics alone.
Please let me know if I am wrong and why. Also, please excuse in advance any weird formalism or jargon: I am not a mathematician, so I am making up words and symbols as I go. I will make sure to define these things to the best of my possibilities though, so that they should be at least clear.
Setting and basic notation
Let me first start by doing a small change of names: from now on, Mark will be called Alice and Rose will be called Bob. The reason for this change is that Alice and Bob are way more famous logicians than Mark and Rose, and it's well known that Alice always goes before Bob (using M and R I always kept forgetting who was going first, also I use M for "morning" so the original choice of names was confusing to me). So, Alice is the one that can see 12 bars and starts guessing first, Bob is the one who can see 8 bars and guesses for second.
With that being said, let me define a few things just to be on the same page.
Let me call $k_0$ this piece of knowledge: Alice and Bob can see all the bars without overlapping and they both will be freed according to procedure X if at least one of them guesses the total number of bars.
For the moment, I prefer to leave the procedure X with which they are freed still undefined: X can be "they are freed immediately" or "they are freed one at a time when the logician visits them" or some other procedure. The reason for leaving X undefined is because although X has implications on how quick Alice and Bob can infer things from what happens to them (e.g. immediately vs the next day, in the evening, etc), it doesn't really change the types of inference that they can make (I promise this will be clearer in a little bit, please bear with me for now).
The other piece of knowledge I want to define is $k_1$: there are either 20 or 18 bars in total.
I prefer not to include $k_1$ in $k_0$ because depending on how we interpret the setup of the problem, $k_1$ and $k_0$ may actually be given to Alice and Bob at different times: once again, this will have consequences on how quickly Alice and Bob will be able to infer things, but not the things that they will be able to infer.
Finally, I want to define $a$ as number of bars that Alice sees and $b$ as the number of bars that Bob sees.
The puzzle is indeed solved if either Alice or Bob correctly guess $a+b$.
Logical framework of inferences
Let me now build the logical framing of the problem. In order to make this process as intuitive as possible, I will start with some simple example and then I will generalize. Also, for now I will explicitly disregard the temporal sequence of events and what happens in which day for which prisoner: these details are bound to be different for different interpretations of the setup, i.e. when do Alice and Bob acquire certain pieces of information and for what reason. Instead, I will for now build the logical framework working with "if -> then" conditionals.
Let's start with Alice.
Alice by definition knows how many bars she sees, i.e. she knows $a$, which is equal to 12. If she also knows $k_0$ and $k_1$, she can immediately infer how many bars Bob can see: she will subtract 12 from either 20 or 18, thus inferring that Bob might see either 8 or 6 bars. Let me represent this with the following diagram:
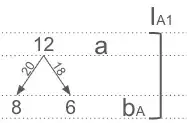
In the above diagram I called $b_A$ the value of $b$ guessed by Alice. Notice that there are 2 possible values for $b_A$, because Alice doesn't know for sure if $a+b$ is 18 or 20. In the above diagram you can track which of these assumptions for $a+b$ leads to which value of $b_A$. I call the collection of all the knowledge and guesses up to $b_A$ inferred by Alice as $I_{A1}$: this is the first inference that Alice can make based on the basic knowledge $\{k_0,k_1,a\}$. Let me represent this fact with the notation
$\{k_0,k_1,a\} \rightarrow I_{A1}$
With the above notation I mean that the set of knowledge $\{k_0,k_1,a\}$ is both necessary and sufficient to make the inference $I_{A1}$.
Similarly if Bob has the set of knowledge $\{k_0,k_1,b\}$, he will be able to make his first inference $I_{B1}$, by using his basic knowledge to guess how many bars Alice sees, i.e. $a_B$. Bob's diagram for $I_{B1}$ looks like this:

and corresponds to the rule
$\{k_0,k_1,b\} \rightarrow I_{B1}$
So far so good. Now here's a question: can Alice infer anything else if she only knows $\{k_0,k_1,a\}$? for example, another thing Alice could try to guess is what Bob might think that the number $a$ is, or in other words she might try to guess what $a_B$ is. Let me call this quantity $a_{BA}$: reading from right to left, this is what Alice thinks that Bob thinks that $a$ is. In order for Alice to guess $a_{BA}$, in addition to $\{k_0,k_1,a\}$ she must also know that Bob is in the position of being able to make an educated guess about the number $a$. In other words, in order to guess $a_{BA}$, Alice must have the knowledge that the inference $I_{B1}$ was made by Bob. If that's the case, Alice's inference diagram expands to the level $I_{A2}$, which comprises all the knowledge that Alice has up to her guess of the quantity $a_{BA}$:

The knowledge rule for $I_{A2}$ can be expressed as
$\{k_0,k_1,a,[I_{B1}]\} \rightarrow I_{A2}$
where the notation $[Y]$ means "knowledge that $Y$ exists". Notice that knowing that $Y$ exists doesn't mean knowing what $Y$ is: just that $Y$ exists. If Alice knows that $a_B$ exists in Bob's mind, even if she doesn't know what its value is, she can still try to guess it. If she doesn't know or can't be sure that $a_B$ exists in Bob's mind, computing $a_{BA}$ would be either futile or impossible.
Notice that there are four possibilities for $a_{BA}$ because there were two possibilities for $b_A$. In other words, Alice doesn't know how many bars Bob sees: it can be 8 or it can be 6. Therefore she must account for the possibility that Bob might have subtracted 8 or 6 from either 20 or 18. Of these 4 possible values however, 2 of them are are the same: these are the values coming from using the same value of $a+b$ to calculate $b_A$ and $a_{BA}$, which both return the value $a$ by definition. Because of this, there are only 3 different possibilities for $a_{BA}$.
Similarly, if Bob knows that Alice was in the position to make the inference $I_{A1}$, he can make the inference $I_{B2}$ according to
$\{k_0,k_1,a,[I_{A1}]\} \rightarrow I_{B2}$
Which produces the tree

Notice also that Bob's inference tree for $I_{B1}$ is indeed contained in Alice's inference tree for $I_{A2}$: since both prisoners are perfect logicians, Alice is definitely capable of accounting for the real guesses that Bob made starting from the true value of $b=8$, together with other possibilities that Bob isn't aware of coming from her other guess of $b$ being 6, although of course she doesn't know which subset of her tree is Bob's tree. However we - the external observer - know which side of Alice's inference tree corresponds to Bob's inference tree, so for the sake of convenience we can visualize both trees together in the following diagram
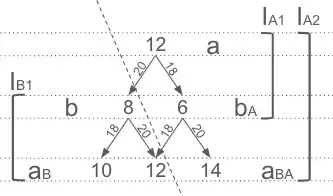
where the dashed line marks our knowledge of the true values of $a$ and $b$ as external observers: the portion under the dashed line corresponds to Bob's inference tree, while the part above it is the part of Alice's tree that Bob cannot know.
At inference level 2 for both Alice and Bob, the overall tree looks like this:
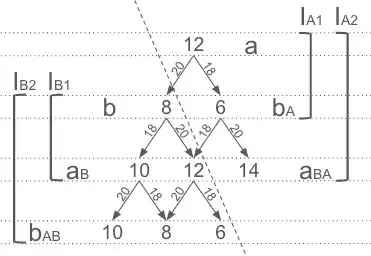
and at inference level 7 for Alice and 6 for Bob the tree looks like this:
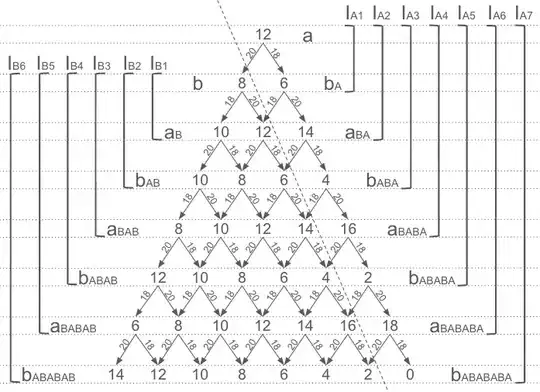
The general rule for any of Alice's inferences can be expressed as:
$\{k_0,k_1,a,[I_{Bn}]\} \rightarrow I_{A(n+1)}$
and similarly Bob's inferences follow the rule
$\{k_0,k_1,a,[I_{An}]\} \rightarrow I_{B(n+1)}$
where $[I_{B0}]$ and $[I_{A0}]$ are the trivial knowledges of either prisoners that the other one knows their own number of bars.
The above diagram and rules constitute the basic logical framing of the problem. The next steps are figuring out: 1) at which moment in time Alice and Bob are capable of making any of their inferences and 2) which of these inferences, if any, would give either prisoner absolute certainty on the value $a+b$.
Information received over time
Let me first start with the problem of the timing of the inferences.
As I mentioned earlier, the timing at which Alice and Bob receive the necessary information to make any inference depends on the rules of the riddle, which also include the procedure X by which they are freed.
Imagine for example that the logician communicates the rules on their first visit to either prisoner and that the prisoners are freed only when the logician visits them (and not immediately), so that for example Bob needs to wait for the night visit even if Alice guessed correctly during the morning. In addition to that, let's also assume that Alice and Bob don't know in advance when and if the logician will visit each of them again: the logician tells either prisoner that he visited the other prisoner only after the visit has taken place.
In this case it's simple to track what Alice and Bob can infer at each moment in time. Let me call Mj and Nj the morning and night of day j.
According to these rules, at M1 Alice knows $k_0$, $k_1$ and of course $a$, so she can immediately make the inference $I_{An}$. Bob However only knows $b$ at this point, because the Logician hasn't visited him yet, so he can't make any inference. we can represent this situation in the following table
| Time |
Alice's knowledge |
Bob's knowledge |
| M1 |
$\{k_0,k_1,a\} \rightarrow I_{A1}$ |
$\{b\} \rightarrow 0$ |
At N1, Alice's knowledge doesn't change because she doesn't know whether the the logician is visiting Bob and even if that would be the case, she would not know if Bob had guessed correctly until the next morning (because in this variation of the riddle the logician doesn't free the prisoners immediately but on his next visit). As for Bob, the logician communicates the pieces of knowledge $k_0$, $k_1$ and the fact that he visited Alice in the morning asking the same question to her. From this last bit of information, now Bob can safely infer that Alice - being a perfect logician - must have made the inference $I_{A1}$. He also can be sure that Alice could have not made any further inference, because he knows that Alice cannot possibly know for sure that the logician is visiting him now. Therefore at N1, Bob is capable of directly making the inference $I_{B2}$. This adds a new line in our table
| Time |
Alice's knowledge |
Bob's knowledge |
| M1 |
$\{k_0,k_1,a\} \rightarrow I_{A1}$ |
$\{b\} \rightarrow 0$ |
| N1 |
$\{k_0,k_1,a\} \rightarrow I_{A1}$ |
$\{k_0,k_1,b,[I_{A1}]\} \rightarrow I_{B2}$ |
On M2 the logician visits Alice again and tells her he visited Bob the night before. Given that the logician is not freeing Alice, she knows for sure that Bob didn't solve the riddle, however this is a trivial piece of information because she already knows by the nature of the logician's riddle that Bob's guess of $a$ must have two choices. She of course doesn't know which two choices out of the three possible guesses she has for $a_{BA}$ are Bob's guesses, but at least she can now make the inference $I_{A2}$. In addition to that, she also knows that Bob had enough knowledge to make the inference $I_{B1}$, so she can directly make the inference $I_{A3}$, which already contains $I_{A2}$. On the other hand, Bob is oblivious to all this, so he hasn't gained any new piece of knowledge. The summary table now looks like
| Time |
Alice's knowledge |
Bob's knowledge |
| M1 |
$\{k_0,k_1,a\} \rightarrow I_{A1}$ |
$\{b\} \rightarrow 0$ |
| N1 |
$\{k_0,k_1,a\} \rightarrow I_{A1}$ |
$\{k_0,k_1,b,[I_{A1}]\} \rightarrow I_{B2}$ |
| M2 |
$\{k_0,k_1,a,[I_{B2}]\} \rightarrow I_{A3}$ |
$\{k_0,k_1,b,[I_{A1}]\} \rightarrow I_{B2}$ |
On N2 a similar reasoning applies for Bob, which is now aware that Alice made the inference $I_{A3}$, so he can make the inference $I_{B4}$
| Time |
Alice's knowledge |
Bob's knowledge |
| M1 |
$\{k_0,k_1,a\} \rightarrow I_{A1}$ |
$\{b\} \rightarrow 0$ |
| N1 |
$\{k_0,k_1,a\} \rightarrow I_{A1}$ |
$\{k_0,k_1,b,[I_{A1}]\} \rightarrow I_{B2}$ |
| M2 |
$\{k_0,k_1,a,[I_{B2}]\} \rightarrow I_{A3}$ |
$\{k_0,k_1,b,[I_{A1}]\} \rightarrow I_{B2}$ |
| N2 |
$\{k_0,k_1,a,[I_{B2}]\} \rightarrow I_{A3}$ |
$\{k_0,k_1,b,[I_{A3}]\} \rightarrow I_{B4}$ |
As the logician keeps visiting Alice and Bob, the inference table keeps expanding with the same pattern
| Time |
Alice's knowledge |
Bob's knowledge |
| M1 |
$\{k_0,k_1,a\} \rightarrow I_{A1}$ |
$\{b\} \rightarrow 0$ |
| N1 |
$\{k_0,k_1,a\} \rightarrow I_{A1}$ |
$\{k_0,k_1,b,[I_{A1}]\} \rightarrow I_{B2}$ |
| M2 |
$\{k_0,k_1,a,[I_{B2}]\} \rightarrow I_{A3}$ |
$\{k_0,k_1,b,[I_{A1}]\} \rightarrow I_{B2}$ |
| N2 |
$\{k_0,k_1,a,[I_{B2}]\} \rightarrow I_{A3}$ |
$\{k_0,k_1,b,[I_{A3}]\} \rightarrow I_{B4}$ |
| M3 |
$\{k_0,k_1,a,[I_{B4}]\} \rightarrow I_{A5}$ |
$\{k_0,k_1,b,[I_{A3}]\} \rightarrow I_{B4}$ |
| N3 |
$\{k_0,k_1,a,[I_{B4}]\} \rightarrow I_{A5}$ |
$\{k_0,k_1,b,[I_{A5}]\} \rightarrow I_{B6}$ |
| M4 |
$\{k_0,k_1,a,[I_{B6}]\} \rightarrow I_{A7}$ |
$\{k_0,k_1,b,[I_{A5}]\} \rightarrow I_{B6}$ |
So finally, on the morning of the 4th day, Alice is capable of making the inference $I_{A7}$. This inference (together with inference $I_{A6}$) is important because it's the first inference in the sequence which contains an impossible value. I will discuss later the consequences of this. For now it's important to notice that the only reason why each passing of morning or night is capable of conveying information to Alice and Bob is because in this version of the puzzle they did not have this information beforehand: they don't know if and when the logician will visit each of them next, and they would not know right away if the other person gave the right answer. They have to wait for the logician's visit to gather the knowledge that the other prisoner got the necessary knowledge to make a guess, and only at that point they can update their next guess, thus advancing along their inference tree.
Now, what would happen if - as it is stated in the riddle - the logician communicates the all the rules to the prisoners (including when he will visit them) right away on day 1? In this case both Alice and Bob will have on day 1 not only the knowledges $k_0$, $k_1$ and either $a$ or $b$, but they would also immediately know that the other prisoner has knowledge of all this. In other words, they will be able to compute their respective inference trees at any level with absolute certainty from the moment they are told the rules. In this case, the passing of time and the visits of the logician would not covey any new piece of information that they don't already have, so they won't gain any new information whatsoever on any future day that they don't already have on day 1.
So in the actual version of the puzzle, Alice and Bob are either capable of solving the riddle on day 1, or they will never be able to solve the riddle on any other day.
with that in mind, let's now see if Alice and Bob can solve the riddle with the information they can access.
Impossibility of solving the riddle
As I mentioned before, inferences $I_{A6}$ and $I_{A7}$ mark an important milestone in that they are the first inferences which contain an impossible guess. Inference $I_{A6}$ contains the guess 18 for the value of $a_{BABABA}$ and 0 for the value of $b_{ABABABA}$. So, what does that mean?
Before going deeper into the meaning of this, notice that inferences $I_{A6}$ and $I_{A7}$ having the guesses 18 and 0, made by Alice in the morning of the 4th day echoes the solution given by Joe in his highlighted post. However one problem is that in order to get M4 as the critical day, I had to change the setup of the problem and having the logician withholding a lot of information from the prisoners, so that every visit of the logician would actually convey useful information that the prisoners didn't have beforehand. The other problem is that Joe's solution only accounts for 1 out of either 7 (for $I_{A6}$) or 8 (for $I_{A7}$) possibilities. Although Alice can indeed safely discard the illogical guesses of 18 or 0, she can't discard all the other equally possible options.
In other words, even being able to make inference $I_{A6}$ or $I_{A7}$ and discarding one value out of their pools, won't give Alice any certainty on which other value she should keep or discard. Growing the inference tree further would eventually produce more impossible values, in both Alice and Bob's inference trees; at the same time there will always be multiple good values which could all be equally possible.
Because of this, the riddle is not possible to be solved by Alice and Bob using pure logic alone.
The reason why the previously proposed solutions work is because Alice and Bob are unconsciously following a strategy to communicate useful information to each other with every visit of the logician.
Imagine for example that on day 1, after they are told the rules of the riddle but before they know how many bars they will see in their respective cells, Alice and Bob have the possibility to strategize. They can agree that with each of the logician's visit they will count down from either 20 or 18 until they reach the number of bars that they see. In this scenario, every visit of the logician that doesn't result in being freed communicates to the each prisoner information about the number of bars that the other prisoner sees. But this is true ONLY because Alice and Bob decided to follow a precise strategy which they agreed beforehand: the strategy is what assigns a meaningful information to the logician's visit, not pure logic alone.
If Alice an Bob are not allowed to strategize, relying only on pure logic would not grant them to follow any of the strategies proposed by any of the solutions. This is true as long as a coherent and logical framing of this riddle which does not guarantee any solution exists, like the one I proposed here. Unless I committed some logical fallacy in my framing, one must admit that a perfect logician may actually use the same framing as the one I proposed, given that my framing can be obtained by perfect logics alone. Even if the strategies proposed in any of the solutions are also logical, Alice and Bob would not be guaranteed to automatically follow any of them without strategizing first or somehow choosing to follow the same logics by total serendipity.
If there was only a unique strategy that can guarantee a win, or if all the possible strategies that would guarantee a win would have the same outcome (e.g. Alice finding that Bob has 8 bars on the morning of the 4th day), Alice and Bob being perfect logicians would be able to identify and implement this unique strategy (or decide to implement any of the equivalent strategies) without previously agreeing with each other, as this would be the most logical thing to do to be freed. The fact that multiple successful strategies exists to solve the riddle on different days already implies that Alice and Bob can't know for sure which of these strategies the other will implement. One could argue that the strategy which would guarantee the earliest freeing time would be the best choice and should therefore automatically implemented by Alice and Bob. But given that with any of these strategies Alice and Bob gain information over time and don't know in which day they would gather the necessary information to solve the riddle, I argue that it's not possible for them to identify with absolute certainty a strategy that is a priori superior to the others. In addition to that, given that in theory multiple strategies can be devised to solve the problem and given that perfect logicians are not omniscent beings but mere humans, logics suggests that both Alice and Bob needs to account for the possibility that the other person might devise a better strategy than any of the strategy that they are currently thinking about. In other words, blindly deciding to choose a strategy without aligning with the other prisoner first would be the same as making a random choice. Assessing the probability of success of this random choice is also not possible (because Alice and Bob cannot know for sure how many successful strategies the other is thinking about), which means that choosing to follow a strategy may be just as good or possibly even worse than just randomly pick one of the two numbers proposed by the logician. And in any case, even if deciding to blindly follow a strategy would somehow guarantee a better chance of success than randomly picking one of the two numbers, success would still not be guaranteed with absolute certainty.
Because of this, even if Alice and Bob can in principle solve the riddle by strategizing beforehand and making perfectly logical decisions coherently with their chosen strategy, in the most general case of following only pure logic nothing guarantees that they will have enough information to solve the riddle at any point in time.
Therefore the riddle is unsolvable with absolute certainty.









