Is it possible to scramble a Rubik's cube such that no two squares of the same color are touching?

Question

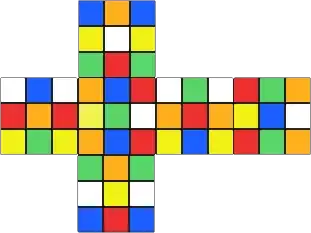
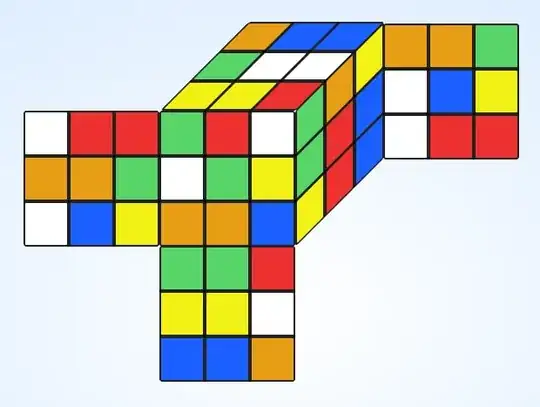
My friend always insists on scrambling my Rubik's cube "perfectly" before giving it to me to solve. According to his definition, a "perfect" scramble must have no three of the same color touching (which takes an annoyingly long time to achieve). For example, this scramble is not a perfect one (showing the front face only):

RRG
BRB
YWO

because three red squares are touching, while this one is perfect:

RRG
BBR
YWO

Is it possible to achieve a scramble where no two same-colored squares are touching, on all sides?

My dad once achieved this. He took a cube and scrambled it, then somehow managed to arrange it so that it followed this rule. I have no idea how he did it, but he could probably do it again. — Justin, Jun 09 '14 at 07:50
Another method is to imagine breaking the cube into the 20 pieces, then putting them together ensuring there is no two same-colored squares touching. While this reunited cube might not be solvable, there is a high chance that it will, and try "solving" a solved cube into your imagined one. I used to do that to create patterns of letters on each side of the cube to create a name. — justhalf, Sep 01 '14 at 08:07
Oops, based on http://puzzling.stackexchange.com/questions/525/how-many-distinct-unsolvable-rubiks-cubes-exist it's not really a high chance, but 8.3% — justhalf, Sep 01 '14 at 08:14
I believe a so-called "perfect" scramble is a bit easier to solve. If a color matches but ony partially, in the wrong place, it is a bit confusing and you might need to dislodge the piece before putting it in the right place. It seems to me if the colors never match, pieces can be put in place with less moves on average. — Florian F, Oct 12 '14 at 20:43
I know this is old, but I just wanted to chime in and say that I managed to get a cube with no two of the same color touching, including diagonals, fairly easily. All you need to do is solve a cube the normal way but flip the direction of edge pieces and swap the corner pieces to the opposing face. I'd be glad to post pictures if anyone's interested, but I don't have any ATM. — user193860, Jun 08 '15 at 02:36
This is quite easy to do, without even following any particular algorithm, just making logical moves while looking at a cube. I've done it today about 12 times in the past hour without putting much thought into it. — Reverse Engineered, Jun 25 '23 at 06:47

score 40 · Accepted Answer · edited Feb 23 '21 at 12:13

40

Yes.

Examples:

Superflip

"Checkerboard"

edited Feb 23 '21 at 12:13

melfnt

5,132
2
13
58

answered May 27 '14 at 14:45

Kendall Frey

3,383
23
27

The checkerboard is solvable with U2 D2 R2 L2 F2 B2. And I forget how to solve the superflip, but it's one of the examples of an arrangement that takes 20 moves to solve. – May 27 '14 at 14:55
2

@JoeZ. reverse U R2 F B R B2 R U2 L B2 R U' D' R2 F R' L B2 U2 F2 – ratchet freak May 27 '14 at 14:59
The checkerboard one has a broken URL for me – John Dvorak May 28 '14 at 14:15
@JanDvorak I've switched it to imgur. – Kendall Frey May 28 '14 at 14:26
This is technically not a scramble; this is a pattern. With a specific sequence of moves, the cube could easily be put right again. A scrambled cube is more random than that. – Brian J. Fink Jun 05 '14 at 00:16
1

@BrianJ.Fink What exactly is the definition of a scramble? Also, http://dilbert.com/dyn/str_strip/000000000/00000000/0000000/000000/00000/2000/300/2318/2318.strip.gif – Kendall Frey Jun 05 '14 at 00:23
In my understanding, a scramble is a state of randomness of arrangement, sufficient to make the solution of the puzzle a challenge. Your first example was better than your second; however, all the corners remain in place in both examples. This, as I understand patterns and scrambles, is not the latter, but the former. – Brian J. Fink Jun 05 '14 at 00:35
Both of them are legal WCA scrambles There's no special property about either cube that distinguishes it from being a scramble, as far as I know. And it's trivial to make a few turns to either to make it 'more scrambled' (as you might say). – Kendall Frey Jun 05 '14 at 00:40
Well whether the fit the WCA's definition or not, they are weak scrambles at best, imho. – Brian J. Fink Jun 05 '14 at 01:10
See the following for some pattern examples and instructions: https://ruwix.com/the-rubiks-cube/rubiks-cube-patterns-algorithms/ – brichins Jan 05 '17 at 17:29

score 7 · Answer 2 · edited Feb 23 '21 at 12:18

While it's somewhat pattern based, I managed to produce the following by

doing a series of rotating opposing flips (e.g. flipping left and right counterclockwise simultaneously, switching faces between each flip):

        Y O Y
        G R B
        W O W
        - - -
G W G | R Y R | B Y B | R W R
O B R | G W B | O G R | B Y G
G Y G | O Y O | B W B | O W O
        - - -
        W R W
        G O B
        Y R Y

I'm relatively new to seriously trying to figure out how to solve these things, so I don't know if this is the same as the above mentioned superflip or not. Technically it's a pattern, however without being aware of the pattern there's little to obviously suggest it was in any way intentional the way some other patterns do.

score 2 · Answer 3 · edited Oct 19 '21 at 20:45

2

Yes, but I was able to shuffle it further without the checkerboard pattern so it even looked random!

edited Oct 19 '21 at 20:45

bobble

10,245
4
32
80

answered Oct 30 '19 at 01:13

Chris

21
1

score 1 · Answer 4 · edited Oct 19 '21 at 15:59

1

R2 L2 U2 D2 F2 B2 R L F B R' L'

No sides should touch.

edited Oct 19 '21 at 15:59

Hazel へいぜる

10,581
15
74

answered Mar 23 '15 at 21:13

Abby

21
1

Sweet and simple. $(+1)$ – Mr Pie Jul 05 '18 at 12:55

Florian F · Answer 5 · 2021-10-19T21:05:40.017

I'd like to present my "anti-solved" solution.

A solved cube is boring. This is how I now arrange my cube when I don't use it.

or

It has the properties:

No two squares with same color touch orthogonally. Not even over an edge.(*)
No two squares with same color touch diagonally on a face.
(I couldn't avoid squares touching diagonally over an edge.)
Each color is present once or twice on each face.
Each combination of 4 colors is present twice on 4 adjacent squares, possibly over an edge.

(*) Especially proud of that last part. :-)

PS: oops! I posted the same pattern already on another thread...

score 1 · Answer 6 · edited Oct 19 '21 at 15:59

1

Alright - here it is. Mystery solved. Merry Christmas!

L2 D B2 L2 B2 D2 F2 U L2 F2 L’ R’ U’ B2 F2 R B’ R B’ F2

edited Oct 19 '21 at 15:59

Hazel へいぜる

10,581
15
74

answered Dec 25 '19 at 15:49

Jeff Irick

11
1

Took a second picture showing the other three sides below. – Jeff Irick Dec 25 '19 at 15:54

score 0 · Answer 7 · answered Mar 03 '24 at 03:21

Here is my perfect scramble. This has:

Every color on every face.
No more than two of any color on a face.
No two squares of the same color touching side-by-side on any face.
No two squares of the same color touching on a corner on any face.
No two squares of the same color touching on a corner where two faces meet.
A different pattern on every face.

To create it: D2 F2 R2 D2 L2 U F2 U' F' U F2 U' R2 B' F R' D2 F' D' L

To solve it: L' D F D2 R F' B R2 U F2 U' F U F2 U' L2 D2 R2 F2 D2

Since you can start with the cube in any one of 24 different orientations and since you can do the moves or the mirror image of the moves, there are 48 unique arrangements produced by this pattern.

This is the only solution that meets all of the above criteria.

The program that I wrote to find this solution is available here: https://github.com/telemath/PerfectScramble.

score 0 · Answer 8 · edited Oct 19 '21 at 16:01

0

Starting from a solved, standard Rubik's Cube (3x3x3) apply this sequence of moves to produce a configuration that meets this condition: no two squares of the same color will touch side-by-side.

R2 L2 U2 D2 F2 B2 R L F B R' L'

The apostrophe indicates a counter-clockwise turn

This sequence also ensures each of Rubik's 6 colors are represented on all 6 sides at once. These are two things I've been wanting to achieve, in just one sequence of moves.

edited Oct 19 '21 at 16:01

Hazel へいぜる

10,581
15
74

answered Mar 22 '16 at 07:26

Derek

1

2

This is a little hard to follow. I assume you are starting from a solved cube and the apostrophe indicates rotating counter-clockwise. I believe you are claiming that this sequence of moves applied to a solved cube will produce the configuration described in the question. If you could edit and add these details, and perhaps show a face of the cube after these moves it would help a great deal. Thanks! – Hugh Meyers Mar 22 '16 at 08:18
Yes, I'm starting from a solved, standard Rubik's Cube (3x3x3) and the apostrophe does indicate a counter-clockwise turn. Yes, the sequence applied to a solved cube produces the configuration described in the question, ie no two squares of the same color will touch side-by-side. – Derek Mar 22 '16 at 10:47
Challenge 1: Find a sequence of 8 moves that achieves your goal (every side has every colour). Challenge 2: Find a sequence of 7 moves. – user21820 Apr 29 '17 at 18:06

Cloudy7 · Answer 9 · 2019-10-30T06:56:40.497

0

EDIT: My answer was based on a misinterpretation of the question, and will be fixed when I can find time. My apologies.

Yes. Such a position is achievable with the following set of six moves:

R U L D R U

This solution guarantees that all six colors are present on each face, in a constant ratio of 2:2:2:1:1:1. The following image of the result below is courtesy of the website https://rubiks-cu.be/.

edited Oct 30 '19 at 06:56

answered Oct 30 '19 at 04:24

Cloudy7

1,942
9
27

1

You've got two touching. – JMP Oct 30 '19 at 05:47
@JMP The OP only wants to avoid 3 touching. – Jaap Scherphuis Oct 30 '19 at 06:02
4

OP says: Is it possible to achieve a scramble where no two same-colored squares are touching, on all sides? @JaapScherphuis – JMP Oct 30 '19 at 06:03
You're right, I misread it. – Jaap Scherphuis Oct 30 '19 at 06:06
And so did I. I will continue working on a solution. – Cloudy7 Oct 30 '19 at 06:26

Is it possible to scramble a Rubik's cube such that no two squares of the same color are touching?

9 Answers9

Linked