4 Gridded Prime Numbers

Question

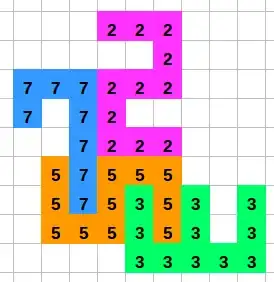
You have the first four prime numbers ($2$,$3$,$5$ and $7$) which are gridded and shown as below:

You are trying to get highest total score you can reach with arranging the numbers by rotating (no reflection allowed) them without overlapping them on each other.

The total score is calculated how many lines are joint after arranging and multiplying how many joints you got with the actual prime number and take the sum of all gridded prime number scores at the end. For example, if this question was asked to arrange the first two prime numbers ($2$ and $3$), the answer would be as below:

Since there are 8 lines of the grid are touched with each other, the total score would be $2\times8+3\times8=40$ which is the maximum score you can get with $2$ and $3$.

Note: I am very sorry to let you know there is better answer than 172. That's totally my mistake!

It is definitely not clear how score is computed. Ah Got It, when you mentioned 8 lines you should have noted that the picture is actually also 8 lines high. XD — CoffeDeveloper, Sep 13 '16 at 10:32
i'm sorry...did you mean to say "there is no better answer than 172"? — max8126, Jun 05 '17 at 20:08

Matsmath · Accepted Answer · 2016-09-10T21:44:32.760

12

I have 172, with the correct tiles.

edited Sep 10 '16 at 21:44

answered Sep 10 '16 at 21:04

Matsmath

1,929
2
12
30

also, just rotate the 2 clockwise 90 degrees for an extra 5 points – astralfenix Sep 10 '16 at 21:27
1

For anyone interested in trying to beat this, I made a spreadsheet to make it easier to play around with. Make a copy for yourself and try to beat 172! – GentlePurpleRain May 30 '17 at 15:29
Thanks for that spreadsheet. I tried lots of combinations but I have no idea how to get more than 172. – Arthur Dent May 30 '17 at 21:53
@GentlePurpleRain Nicely made! I wrote a small macro to utilize the spreadsheet and brute-force possible solutions. Can't get past 172. – max8126 Jun 05 '17 at 20:06

score 3 · Answer 2 · answered Sep 23 '16 at 07:53

3

I believe the maximum is

172

Otherwise I think the maximum cannot be found by a greedy approach (trying to maximize the contact point between numbers.

My alternative solution to Matsmath:

answered Sep 23 '16 at 07:53

CoffeDeveloper

476
1
4
16

2

Isn't your solution the same as mine, just rotated 180 degrees (essentially: turned upside down)? – Matsmath Sep 23 '16 at 08:56
1

oh men, you are right. I spent 1 hour on that - – CoffeDeveloper Sep 23 '16 at 10:56

Crazy Cucumber · Answer 3 · 2017-06-02T18:28:05.317

2

I got

176

With this formation:

edited Jun 02 '17 at 18:28

answered Jun 02 '17 at 18:21

Crazy Cucumber

179
4

7 is wrong shape. – Oray Jun 02 '17 at 18:23
Alright, how about now? Edited the answer – Crazy Cucumber Jun 02 '17 at 18:28
@Oray interchanged 5 and 2 because 2's rotation just did not seem right. Score is still the same. – Crazy Cucumber Jun 02 '17 at 18:35
2

How is this accepted and bountied when the 7 is reflected, which the puzzle statement expressly does not allow? @Oray – Rubio Jun 02 '17 at 23:10
@Rubio that's totally my mistake sorry :/ – Oray Jun 03 '17 at 05:52
@Rubio I did not notice that. I apologize. – Crazy Cucumber Jun 05 '17 at 13:09
@Oray Is it still correct that there is an answer that is more than 172, with no reflection allowed? – max8126 Jun 05 '17 at 14:21
You could just reflect the entire thing. – Deusovi Jun 05 '17 at 17:32
@Deusovi If you reflect the entire thing, 2 and 5 would swap place and the score will be lowered (158). – max8126 Jun 05 '17 at 18:40
@max8126: Ah, good point - my mistake! – Deusovi Jun 05 '17 at 19:04

Jonathan Allan · Answer 4 · 2016-09-13T09:57:04.793

1

I have

$166$

With

$2\times 6 + 3\times 8 + 5\times 12 + 7\times 10 = 166$

edited Sep 13 '16 at 09:57

answered Sep 10 '16 at 21:26

Jonathan Allan

21,150
2
58
109

that is $69 + 412 + 8*8 = 166$ – Gintas K Sep 13 '16 at 09:49
Yes it should be $166$, I had missed one of the seven edges in the count. – Jonathan Allan Sep 13 '16 at 09:58

score 0 · Answer 5 · answered Jun 05 '17 at 19:43

0

I got

~~182~~ 146

With this formation:

EDIT: Miscalculated the score.

answered Jun 05 '17 at 19:43

Matt

794
3
12

4 Gridded Prime Numbers

5 Answers5

Linked