16 pawns on a chess board with no three collinear: how do I go about solving this?

Question

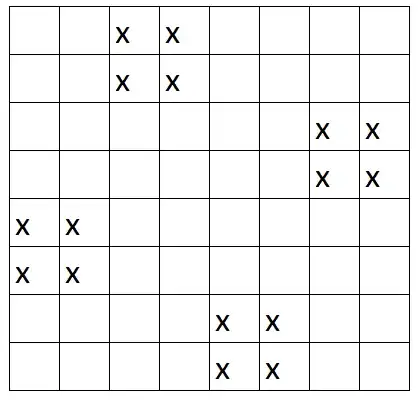
Here's a problem that was posed to me but I haven't seen anything about it anywhere online! I'm beginning to wonder if I'm just getting played!

You have a chessboard and sixteen pawns. The puzzle is to have all sixteen pawns on the board such that no three are collinear (three in a row). It can be considered with Cartesian coordinates; the three pawns can't make the same slope, even at unequal distances (ex: 0,0 & 1,2 & 3,6 is not allowed).

I'm thinking that the solution must be so complex that there must be a logic, strategy, or algorithm for this. Could people help me out? Thanks!

No three (or more) pawns may be in any straight line of any direction. This is a special case of the no-three-in-line problem. Martin Gardner reprints the best-known solutions for all board sizes up to 16x16 in chapter 5 of Penrose Tiles to Trapdoor Ciphers, pub. Freeman, ISBN 0-7167-1987-8. — Rosie F, Sep 06 '16 at 06:22
@Jamal commenting on an answer to this question cites a result from Achim Flammenkamp's web site. The portal to his research on the no-3-in-line problem is here. — Rosie F, Sep 06 '16 at 08:59
ah... but must the pawns follow the chess rules? IE must start in rows 2 and 7 for the appropriate colors? or are all 64 spaces available to all pawns? — xQbert, Sep 06 '16 at 15:38
@JonMarkPerry They cannot be placed on top of each other. Each has their own square. — Steve DSign, Sep 06 '16 at 17:51
I note that you got a number of solutions to the problem but no one actually answered your question: how to go about solving it? The way I would go about solving it is by solving a bunch of simpler problems. Fewer pawns makes it easier, larger board makes it easier. So try coming up with solutions with different numbers of pawns and larger or smaller boards, and see what you learn from solving those easier problems. Maybe you can adapt one of the solutions to an easier problem to solve a harder one. — Eric Lippert, Sep 06 '16 at 21:07

Jamal Senjaya · Accepted Answer · 2017-06-14T03:49:25.683

32

The Algoritm is :

Create a 4x4 table which each 2 pawns cannot be in 1 row, 1 column, and 1 diagonal including those diagonals obtained by "wrapping around" the edges.

Then

Expand it into 8x8 chess board

Here is the complete solution from Achim Flammenkamp Ph.D. There are totally 57 solutions

edited Jun 14 '17 at 03:49

answered Sep 06 '16 at 03:52

Jamal Senjaya

17,864
2
41
147

Ignoring rotations/reflections, is this a unique solution? – greenturtle3141 Sep 06 '16 at 04:41
@greenturtle3141 I do not know, I just find the answer today, with my second hypothesis (my first hypothesis is wrong). Maybe there is another solution. – Jamal Senjaya Sep 06 '16 at 04:44
@greenturtle3141 No. OEIS gives the numbers of inequivalent solutions, i.e. counting congruent solutions as the same, and of all solutions, counting congruent ones as different, of the problem of placing 2n pawns on an nxn board, no 3 in a straight line. For n=8 there are 57 and 380 respectively. For all n>3 there are non-congruent solutions. – Rosie F Sep 06 '16 at 06:17
@greenturtle3141 Since no three pawns are colinear, any two rows or columns can be swapped with each other any number of times, as these operations can never make pawns that aren't already colinear colinear. – Williham Totland Sep 06 '16 at 07:27
@greenturtle3141 Actually, that's wrong; it only applies when diagonals are allowed. – Williham Totland Sep 06 '16 at 07:29
2

check this : http://wwwhomes.uni-bielefeld.de/achim/no3in/no8.gif. It shoes all the solutions in tiny pixels. – Jamal Senjaya Sep 06 '16 at 08:01
I got above link from @RosieF links. – Jamal Senjaya Sep 06 '16 at 08:03
1

@JamalSenjaya Ah, good ol' Achim Flammenkamp, who has contributed so much to this and other areas of mathematics. – Rosie F Sep 06 '16 at 08:16
5

then, "than" is to express a comparison, not a time sequence. – Federico Sep 06 '16 at 10:35
Love this answer, thanks to all who answered and contributed! – Steve DSign Sep 06 '16 at 17:56

score 1 · Answer 2 · answered Sep 06 '16 at 21:02

1

Note that each of the eight rows of the chessboard must contain exactly two pawns. If a row contained 3 or more pawns, it would violate the conditions of the problem. And if a row contained less than 2 pawns, then some other row would have to have 3 or more pawns, again violating the conditions of the problem.

There are 8*7/2 = 28 ways to place a pair of pawns on a given row.

So, with 8 rows, there are only 28^8 = 377x10^9 possible ways of solving the problem. This is a large number but within the realm of a computer search.

answered Sep 06 '16 at 21:02

Seattle

11
1

Starting at the third row, the number of choices will go down rapidly. – gnasher729 Sep 06 '16 at 21:39
2

Since there must be two pawns in each column, you have only one choice for the last row, and only at most six choices for the seventh row. – gnasher729 Sep 06 '16 at 21:45
Is anyone trying this approach, then? – ghosts_in_the_code Sep 14 '16 at 14:55

score -2 · Answer 3 · answered Jul 09 '18 at 05:02

-2

The answer is based on Rotational symmetry.

answered Jul 09 '18 at 05:02

Gayathri

7

Hello, welcome to Puzzling.SE. Can you please add more explanation to your answer. Meanwhile why don't you take the tour to earn your first badge. – u-ndefined Jul 09 '18 at 05:29
1

A8, B6 and D2 are on the same line. (You have the chess board sideways, but luckily the position is symmetrical, so the coordinates work in any orientation.) – Bass Jul 09 '18 at 06:46
Similarly, A1, D2, G3 are collinear, as are F7, G4, H1; B6, E7, H8; and probably others. – Rubio Jul 11 '18 at 18:21

16 pawns on a chess board with no three collinear: how do I go about solving this?

3 Answers3