Chess at the 2020 Olympic Games

Question

For the 2020 Olympic Games, the World Chess Federation asked the Olympic committee to include chess as official sport. The committee agreed under one condition:

The Chess Federation must design a chess-colored black and white logo, consisting of three intersecting Olympic rings with areas 1 each, such that the black area - covered by odd number of rings, is less than 1. It is not necessary that each of the rings intersects all of the others.

Here is an example of one chess-colored black and white logo.

Is chess going to be part of the 2020 Olympic Games?

Remark: I have found a geometric proof of the problem for any 3 central-symmetric convex shapes, but it is not as nice and fun as the one for circles. Also, probably the claim is true for any odd number of C-S C bodies in n-dimensional space. For the related version with squares/regular hexagons, check Black and White. It has a nice combinatorial geometric proof.

HINT 1:

HINT 2:

HINT 3:

HINT 4:

HINT 5:

(((H4=>H2)+H3)=>H1)=>:)

HINT 6:

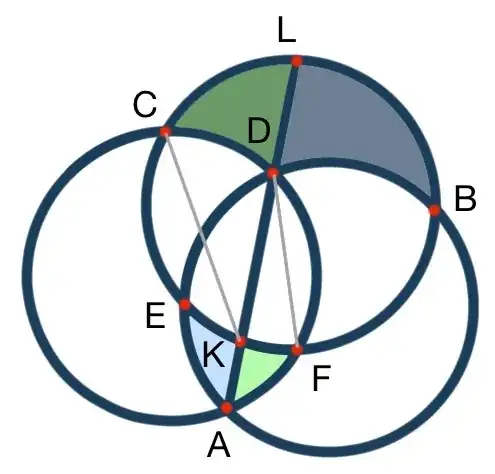
The arrows show relations between arc lengths. Color shades show relations between region sizes. Use HINT 4 to show that the relations in HINT 2 are true for well-chosen pairs of arcs.

HINT 7 (non-cryptic):

If the circles are A, B, and C, and A denotes the area only in A, BC denotes the area only in B and C, etc., then the problem is equivalent to showing that A>BC, or B>AC, or C>AB. The line drawn in HINT 1 separates both A and BC (or B and AC, or C and AB) in 2 pieces each. Can you show that the pieces from BC are smaller than their corresponding pieces from A (or possibly the same, but with BC replaced by AC/AB, and A replaced by B/C)?

HINT 8:

There is some geometry involved, so if you have forgotten what inscribed/inside/outside angles are - http://www.regentsprep.org/Regents/math/geometry/GP15/CircleAngles.htm

Answer 1

The answer is:

No, chess is not going to be part of the Olympic Games.

With one circle, the area covered by an odd number of circles is equal to 1.
With two circles, we can make it range from 0, if the two circles overlap completely, to 2, if they are both completely separate.
When adding a third circle, the amount of area lost plus the amount of area gained must be equal to 1.

This gives us the following equations, where $a$ is the amount of area at the begging and $x$ and $y$ are the amount of area lost and gained respectively:
$0 < a < 2$
$a - x + y < 1$
$x + y = 1$
$0 < x \leq a$

By replacing $y$ with $1 - x$, we have the equation $a - x + (1 - x) < 1$, which means that $x > \frac{a}{2}$. This means that the problem is only possible if a third circle can contain more than half of the area that's covered by only one of two overlapping circles.

Our third circle must overlap both circles, because otherwise, it wouldn't be able to contain even half of the area covered by only one (see this image). The area contained in the third circle is given by: $A \cap C + B \cap C - A \cap B \cap C$. To simplify its calculation, we'll assume that the radii of the circles are $1$ instead of $\sqrt{\frac{1}{\pi}}$, and then multiply the end result by $\frac{1}{\pi}$

The formulas for the areas of intersection of circles with a radius of 1 are:
For two circles: $\pi A = 2\cos^{-1}(\frac{d}{2}) - \frac{d}{2} \sqrt{4 - d^2}$
For three circles (source):
$x_{XY} = \frac{d_{XY}}{2}$
$y_{XY} = \sqrt{1 - \frac{{d_{XY}}^2}{4}}$
$c_1 = \sqrt{(x_{AC} - x_{AB})^2 + (y_{AC} - y_{AB})^2}$
$c_2 = \sqrt{(x_{BC} - x_{AB})^2 + (y_{BC} - y_{AB})^2}$
$c_2 = \sqrt{(x_{BC} - x_{AC})^2 + (y_{BC} - y_{AC})^2}$
$\pi A = \frac{1}{4} \sqrt{(c_1 + c_2 + c_3)(c_2 + c_3 - c_1)(c_1 + c_3 - c_2)(c_1 + c_2 - c_3)}\\\ \ \ \ \ \ \ \ \ + \sum_{k=1}^{3}\sin^{-1}(\frac{c_k}{2}) - \frac{c_k}{4} \sqrt{4 - {c_k}^2}$

Putting these equations into Mathematica and maximizing the area gives us a maximum of 0.5, if the third circle is directly over another one. This means that it's impossible to have a shaded area of less than 1.

Answer 2

Since this problem is possibly a bit too mathematical for Puzzling StackExchange, I decided to post the solution. I believe it contains few interesting ideas, so hope you like it.

It is easy to check that if two of the circles do not intersect each other, the total black area is at least 1. Therefore now we will consider the case when each of the circles intersects both of the others.

Denote the intersection points of the circles with A, B, C, D, E, F, as shown on the diagram above. It is straightforward to check that the following 4 conditions are equivalent:

1. $S_{AEC}+S_{BFA}+S_{CDB}+S_{DEF}\geq 1$
2. $S_{AEC}\geq S_{DFB}$
3. $S_{BFA}\geq S_{DCE}$
4. $S_{CDB}\geq S_{AFE}$

First, notice that $\hat{DC}+\hat{EA}+\hat{BF}=\hat{BD}+\hat{CE}+\hat{AF}$. Simple combinatoric argument shows that there are two consecutive arcs among these, touching at $D$, $E$, or $F$, such that each of them is at least as large as its opposite. Let without of generality $\hat{DC}\geq\hat{AF}$ and $\hat{BD}\geq\hat{EA}$.

Now draw the line AD. Let it intersects $\hat{EF}$ and $\hat{BC}$ at points K and L.

Notice that:

• $\hat{LC}\geq \hat{CD}$
• $\hat{LB}\geq \hat{BD}$
• $\hat{AE}\geq \hat{EK}$
• $\hat{AF}\geq \hat{KF}$
• $\angle{LCD}=\angle{AFK}$
• $\angle{DBL}=\angle{KEA}$

All of these relations follow from simple symmetries and angles in the circles. For example, $\angle{LCD}=\angle{DFB}=\angle{KFA}$, $\hat{LC}=\angle{CKD}\geq \hat{CD}$, and $\hat{AF}=\angle{FDA}\geq \hat{KF}$.

Combining the relations above, we see that:

1. $\hat{LC}\geq \hat{AF}$, $\hat{DC}\geq\hat{KF}$, $\angle{LCD}=\angle{KFA}$

2. $\hat{LB}\geq\hat{AE}$, $\hat{DB}\geq\hat{KE}$, $\angle{LBD}=\angle{KEA}$

Therefore the light green piece $AFK$ can fully fit inside the dark green piece $CDL$, and the light blue piece $KEA$ can fully fit inside the dark blue piece $DBL$. This implies that $S_{CDB}\geq S_{AFE}$, which is exactly point $4.$ from the conditions above.

Answer 3

Partial Answer

Suppose the 3 circles are numbered I, II, and III. Let's denote:

• $A$ is the area that is strictly only inside circle I, but not other circles.
• $B$ is the area that is strictly only inside circle II, but not other circles.
• $C$ is the area that is strictly only inside circle II, but not other circles.
• $AB$ is the area that is inside circle I and II, but not III.
• $BC$ is the area that is inside circle II and III, but not I.
• $CA$ is the area that is inside circle III and I, but not II.
• $ABC$ is the area that is inside circle I, II, and III.

Hence, our target now is minimizing $A + B + C + ABC$.

It is clear that:

• $A + AB + CA + ABC = \text{Area of Circle I} = 1$
• $B + BC + AB + ABC = \text{Area of Circle II} = 1$
• $C + CA + BC + ABC = \text{Area of Circle III} = 1$

Adding the first three equations, we get $A + B + C + 2(AB + BC + CA) + 3ABC = 3$ or $A + B + C + ABC = 3 - 2(AB + BC + CA + ABC)$.

Minimizing $A + B + C + ABC$ is equal to maximizing $AB + BC + CA + ABC$. I'm pretty sure $AB + BC + CA + ABC$ can't be larger than 1 hence $A + B + C + ABC$ can't be smaller than 1.

Anyone have an idea to prove $AB + BC + CA + ABC$ can't be larger than 1? Thanks!

Answer 4

If the logo must be on a flat surface, no, chess will not be a part of the olympic games. If the logo can be on a sphere, however, chess will be a part of the olympic games.

We will start with a sphere of radius R. We will place three circles of radius R*2π / 3 spaced out evenly on the equator (i.e. at -120°, 0°, and +120°, so their edges just barely touch).

The area of each circle is determined by the spherical cap equation:

A=2*π*R*h
R is the radius of the sphere, or 1
h is the height of the spherical cap, or R * (1 - cos(2π/3)) = 1.5 * R
A = 3 * π * R^2

We set the radius of the sphere such that A = 1, so R = sqrt(1 / (3*π)) or about 0.325.

• The area "inside" a single circle, as above, is 1.
• The area "outside" a single circle is, from the same spherical cap formula, 1 / 3.
• When the first circle (circle a) is placed, 1 unit is inside and 1 / 3 unit is outside.
• When the second circle (circle b) is placed, the 1 / 3 of the sphere's surface outside circle b falls within circle a, and vice versa. 2 / 3 units of the sphere's surface area is inside both circles a and b.
• When the third circle (circle c) is places, the 1 / 3 of the sphere's surface outside of circle c falls within the area occupied by circles a and b.

Thus, all of area of the sphere falls either inside all 3 circles (2 triangular-ish pieces covering the poles, for a total of 1 / 3 unit) or inside 2 of the 3 (the area "outside" circles a, b, and c) for a total area of 1 / 3 unit covered by an odd number of circles.

Answer 5

Simple. Something like the logo in the OP, but

with black and yellow counterchanged.

Answer 6

The first thing that came to my mind is

the lunes of Hyppocrates, but I haven't worked on this idea too much. Maybe it leads to a geometric mean - arithmetic mean inequality.