Shown below is a grid of blue and yellow squares with a knight in the upper left hand corner and green square in the lower right hand corner.
Your task is to guide the knight from its starting position to the green square using regulation chess knight moves.
The knight may only visit yellow squares to reach its goal.
Please, in your answer, clearly explain the path taken.
If my Python programming is to be believed, the minimum number of moves required is 41:
It's relatively easy if you start at the exit and try to reach the starting point.
(Apologies for my bad paint skills)
I am 3 minutes late but I think I have a slightly different solution
using a less obnoxious colour
Very late to see this lovely puzzle, but I thought I'd post since
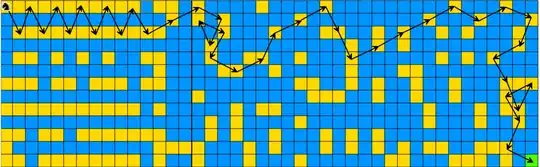
I can confirm that the $41$ move path posted by squeamish ossifrage is optimal.
My code outputs the same path (#may be visited.may not, numbers are the move numbers mod $10$ (to keep to one character, but still allowing easy-ish path following)This path of 41 moves was found:0#2#4#6#8#0.##.3....#....3.........9...1.. .............2.6.4.....2.........8...0...2 .1#3#5#7#9#1#....7...1...#4..#.7..#.#...#. ................5..........#.6.#........3. .##.#.#.#..##...8..#0..#...5......#.#.4... ............#....#9..#.....#...##......... ###.##.###.##..........##..#.#..#..#...5#7 ...............#........###..#..#..#...8.. ###########.#.....#.##...........#...#.#6. ................#.#....#.........#...#..9. ##.##.#######...#.#..#...#.#.#............ #...........####...#.#...#.#.#.#.##..##0.. ##.########.#..#...#...#......##...###.#.1
Python code:
MAZE_TEXT = '''
###########.##.#....#....#.........#...#..
.............#.#.#.....#.........#...#...#
.############....#...#...##..#.#..#.#...#.
................#..........#.#.#........#.
.##.#.#.#..##...#..##..#...#......#.#.#...
............#....##..#.....#...##.........
###.##.###.##..........##..#.#..#..#...###
...............#........###..#..#..#...#..
###########.#.....#.##...........#...#.##.
................#.#....#.........#...#..#.
##.##.#######...#.#..#...#.#.#............
#...........####...#.#...#.#.#.#.##..###..
##.########.#..#...#...#......##...###.#.#'''
def solveDefault():
maze = makeMaze(MAZE_TEXT)
startRow = 0
startCol = 0
endRow = len(maze) - 1
endCol = len(maze[endRow]) - 1
path = solve(maze, startRow, startCol, endRow, endCol)
if not path:
print("No path was found")
return
solvedText = ''
for mazeRow, mazeRowText in enumerate(MAZE_TEXT.strip('\n').split('\n')):
for mazeCol, mazeChar in enumerate(mazeRowText):
if (mazeRow, mazeCol) in path:
solvedText += str(int(path.index((mazeRow, mazeCol))) % 10)
else:
solvedText += mazeChar
solvedText += '\n'
print("This path of {0} moves was found:".format(len(path) - 1))
print()
print(solvedText)
def makeMaze(mazeText):
return [[c == '#' for c in row] for row in mazeText.strip('\n').split('\n')]
def solve(maze, startRow, startCol, endRow, endCol):
if startRow < 0 or startRow > len(maze) or startCol < 0 or startCol > len(maze[startRow]):
raise ValueError("Start location ({0}, {1}) does not exist in the maze provided".format(startRow, startCol))
if not maze[startRow][startCol]:
raise ValueError("Start location ({0}, {1}) is not visitable in the maze provided".format(startRow, startCol))
if endRow < 0 or endRow > len(maze) or endCol < 0 or endCol > len(maze[endRow]):
raise ValueError("End location ({0}, {1}) does not exist in the maze provided".format(endRow, endCol))
if not maze[endRow][endCol]:
raise ValueError("End location ({0}, {1}) is not visitable in the maze provided".format(endRow, endCol))
if startRow == endRow and startCol == endCol:
return [(startRow, startCol)]
reachedByMoves = [dict([(None, [(startRow, startCol)])])]
endLoc = (endRow, endCol)
solved = False
while 1:
newLocs = set()
nextReached = dict()
for prevRC, curRCs in reachedByMoves[-1].items():
for rc in curRCs:
for nextRC in nextLocations(maze, *rc):
if nextRC not in newLocs and not any(nextRC in reached for reached in reachedByMoves[:-1]):
if rc in nextReached:
nextReached[rc].append(nextRC)
else:
nextReached[rc] = [nextRC]
newLocs.add(nextRC)
if nextRC == endLoc:
break
else:
continue
break
else:
continue
break
else:
if nextReached:
reachedByMoves.append(nextReached)
solved = True
else:
break
continue
reachedByMoves.append(nextReached)
break
if solved:
p = [endLoc]
for reached in reachedByMoves[:0:-1]:
for fromRC, toRCs in reached.items():
if p[-1] in toRCs:
p.append(fromRC)
break
else:
raise ImplementationError("Successful path found but not traceable?")
return p[::-1]
def nextLocations(maze, row, col):
for rowDelta, colDeltas in ((-2,(-1,1)),(-1,(-2,2)),(1,(-2,2)),(2,(-1,1))):
newRow = row + rowDelta
if newRow >= 0 and newRow < len(maze):
for colDelta in colDeltas:
newCol = col + colDelta
if newCol >= 0 and newCol < len(maze[newRow]) and maze[newRow][newCol]:
yield newRow, newCol
