There is a reason sudoku uses squares

Question

There exists a 9x9 grid with the cells in one single row numbered 1-9 in order. The cells in the other 8 rows are initially empty.

^{Note: The cells initially containing numbers can be in any one row; not necessarily the first.}

Draw borders to divide the square into 9 non-intersecting continuous regions containing 9 cells each such that you make a sudoku-like puzzle with a unique solution. You may not add any additional numbers or hints. A sudoku-like puzzle, for this question, has the following rules:

• each cell in the 9x9 grid contains exactly 1 integer between 1 and 9 inclusive

• each row and column and bordered region contains each integer between 1 and 9 inclusive exactly once

Answer 1

There is a unique solution to the following

The solution is

Proof of uniqueness

Let us use the following notation:
The rows from top to bottom are given the labels $A-I$
The columns from left to right are numbered $1-9$ (as with the top row).

Firstly, $B9$ must be $1$ since it is the last in its continuous region. Then, this forces $C8$ to be $1$ since none of the rest of row $B$ can contain $1$ nor can column $9$. Similarly, we find that going down diagonally to the left all the entries are $1$ down to $I2$.

Now, look at $C9$. The entry here, $x$, must be the same as $D8$, since its continuous region has to contain $x$ but row $C$ and column $9$ already contain $x$. By a similar line of reasoning, we find, recursively, that the entries $E7$, $F6$, $G5$, $H4$ and $I3$ are all $x$ but of course cannot be $3,4,\ldots,9$ so $x=2$ and $B1$ must also be $2$.

We can continue this line of reasoning, next starting at the entry in $D9$, calling this $y$ and proceeding diagonally left and down to find $y=3$.

In this way, we can fill the entire grid, recursively always beginning at the topmost entry in column $9$.

Answer 2

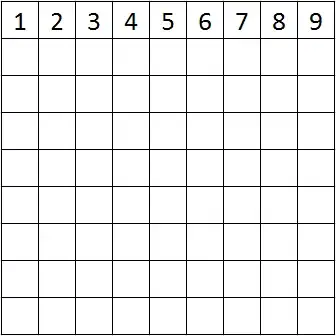
Side notes and footnotes

The Sudoku variation in question turns out to be called “Du-Sum-Oh,” along with some aliases, and cells 1– 8 by themselves can force a unique solution without being given cell 9.

Hexomino’s original answer¹ revealed how delightful this puzzle is but I had forgotten the details months later when mentioning it to a fellow Sudoku enthusiast, so some variety ensued.

^{(Click within a spoiler to reveal it permanently.)}

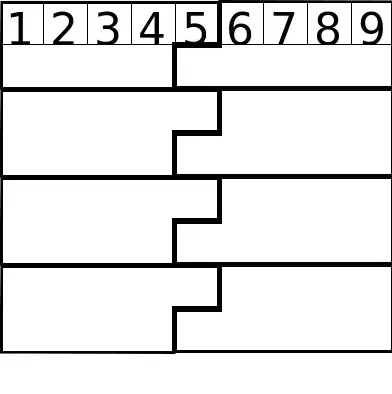
The layout on the left, with straightforward numbering, has a very sleek route to solution ² whereas the numbering on the right demonstrates that an irregular set of initial numbers can also force a unique solution and be amusing to solve^ 3 if you’re in the mood.

Progress came from starting with small boards while experimenting with simple zigzags and L shapes. The 4×4 and 5×5 layouts along the way were misleadingly efficient ⁴ and led to an unnecessarily awkward 9×9 layout.

---

Footnotes (solutions of layouts):

¹ Synopsis of the three stages in Hexomino’s original solution. (Circles ◯ spotlight cells that were most recently filled or are immediately determinable at the steps shown.)

² First and last steps of the present straightforward solution. (Circles ◯ mean the same¹ as above.)

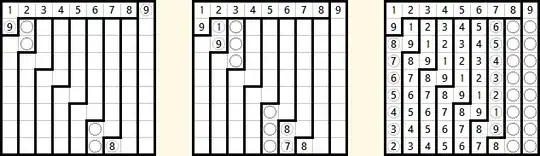
³ Synopsis of a solution for irregularly placed initial numbers. (Circles mean the same¹ as above.)

⁴ Solutions of the 4×4 layout in just two steps and of the 5×5 layout in four steps.

Answer 3

Edit: Angel Koh came up with another solution to my layout, so it is non-unique.

I believe to have a unique solution in regular sudoku you need at minimum: 1 number in each column, 1 number in each row, 1 number in each box, and every number from 1-9. But, you can cheat on 1 of these and for instance satisfy the remaining 3 clues but have a number in 8 boxes.

Has a unique solution which is:


Although I am not sure how to prove it.