45

Mama snake wants to knit a blanket for little baby snake.

She is not a dissipater and wants to make the blanket of a minimal size (area). But her baby snake is quite a lively baby and it always twists and stretches and turns around while sleeping.

If the baby changes position or from, mama takes the blanket and puts it over the baby again.

What size (and form) is the blanket ?

  • The baby snake has the length of 1
  • While sleeping the baby lays on the bed (it's a 2D-puzzle, no 3D)
  • The baby snake can take any shape it wants
    • it can have bends, even sharp bends like 120°
    • it could also be shaped like a wave, a ring or a U-form
    • it could be any shape you can imagine (even a spiral or square)
  • The blanket must always cover any shape of the snake
  • Mama turns and moves the blanket if necessary

mama snake baby snake

Mama snake and her little baby snake

Examples

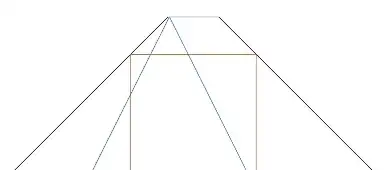
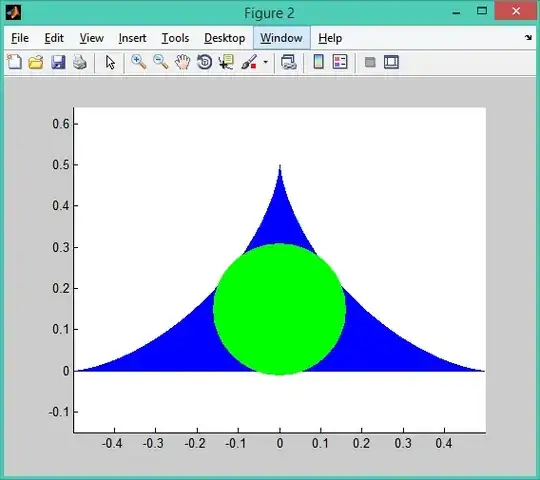
Circle

This is biggest solution (from Miniman):

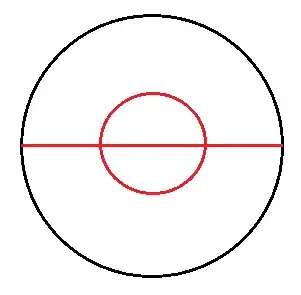
enter image description here

It's a circle with diameter 1 (you can see the red baby snake stretched out totally - and you can also see the baby snake performing a circle).

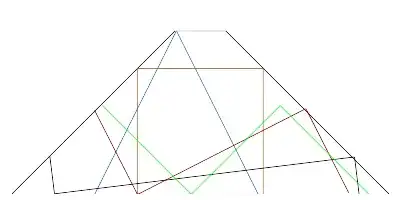
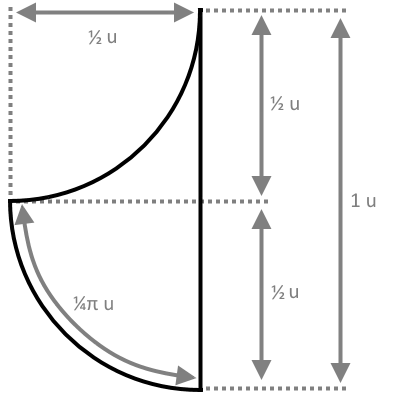
Semicircle small

A smaller version would be a blanket of this size and shape (a semicircle).

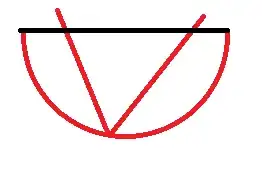
semicircle

You see how the snake performs a bending like a U (red outline) and the resulting size of the blanket (black line). Unluckily this blanket would be too small, because if the snake bends into a 90°L-form it wouldn't fit into the blanket anymore.

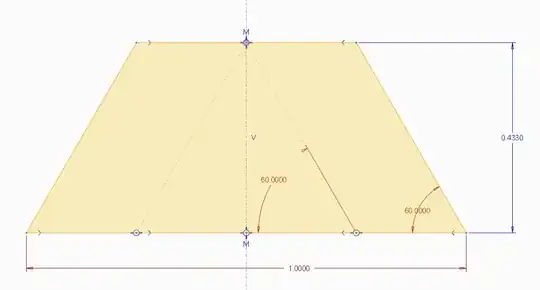
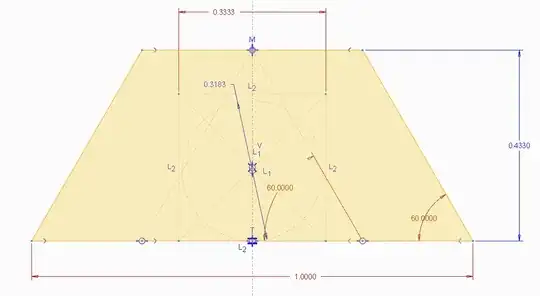
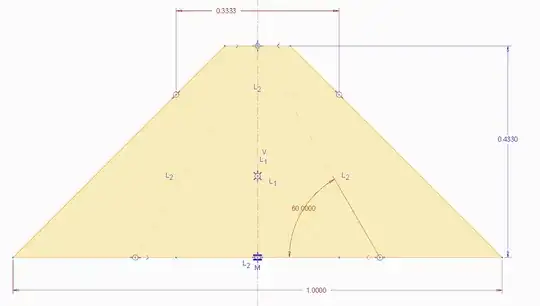
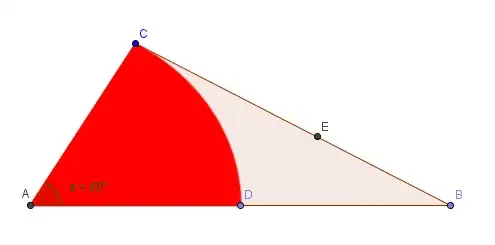
Semicircle big

big_semicircle

That great idea comes from Joe. Thanks for providing that idea! a semicircle with the diameter of 1... This definitely covers the baby snake but as you can see could easily be cut of on several parts...

COTO
  • 10,083
  • 36
  • 91
Martin Frank
  • 731
  • 7
  • 14
  • honestly i heard this puzzle on a radio show and i can't properly remember the solution... – Martin Frank Oct 09 '14 at 04:18
  • yes, right - why haven't you already edited my question?! thanks for giving that hint!! i'll just do it now =) – Martin Frank Oct 09 '14 at 07:41
  • 1
    Is the blanket inflexible? Why not just take a 1x\eps rectangle and bend it as appropriate? – John Dvorak Oct 09 '14 at 08:22
  • 2
    it's not a 'rubber-blanket' @JanDvorak . it can't be stretched and it can't be shrinked, not by any purpose... – Martin Frank Oct 09 '14 at 09:03
  • but *if it would be bendable then it would be the right solution @JanDvorak (i can^t imagine any smaller than)... unluckily it's not bendable :-$ – Martin Frank Oct 09 '14 at 09:04
  • The semicircle image is a bit misleading... the only way the snake could touch the middle of the arc like shown in the picture would be if it made a full 180 degree bend. – Moyli Oct 09 '14 at 10:38
  • it's correct this time ... it referrs to the answer from Joe who wants to cut up the ring and form it into a semicircle. if it's done so you can spread from the middle to the left/right - but you don't reach the end points (i hope you can see this from my pic, it's a bit shoddy, right)... – Martin Frank Oct 09 '14 at 10:41
  • but thinking further the head/tail should look outside of diameter - ill just update it @Moyli – Martin Frank Oct 09 '14 at 10:42
  • 1
    I don't get it. If the snake can fully spread from left to right, then the semicircle's diameter is 1 and radius is 0.5, the same as the snake's length divided by 2, so it has to fold in half. If the semicircle's diameter is less than 1 the snake won't fit under it when fully stretched. – Moyli Oct 09 '14 at 10:44
  • ok, i see what you were aiming at.. i'll add it to the question... @Moyli – Martin Frank Oct 09 '14 at 10:50
  • 1
    I don't know how else you could interpret "cut the circle in half to give you a semicircle with a diameter of 1 unit". – Moyli Oct 09 '14 at 10:50
  • @Moyli right right - i was thinking ahead, sorry... therefore i read too fast, i updated the post, tell me if it's correct now! (thanks for bringin out those little mistakes, this improves the quality of this question) – Martin Frank Oct 09 '14 at 10:58
  • 12
    I think it would be better to just let answers be answers, instead of updating the post to incorporate them all. – SQB Oct 09 '14 at 11:01
  • 4
    You could edit the answers and include the pictures there. – Moyli Oct 09 '14 at 11:04
  • @SQB thanks for your hint, i'll do as you say! (honestly that would definitly make my work easier ^^) – Martin Frank Oct 09 '14 at 11:13
  • @MartinFrank Do you know the correct answer yourself? Otherwise you might want to add an appropriate tag, like [tag:solution-unknown]. – SQB Oct 09 '14 at 11:37
  • i know i know and i @SQB did it already (although not in this thread)... but it's also a source of mistakes, see what happened when i tried to draw Joe's proposal? even if it's not art i would have answers expected to have a minor image, but its not... i'm kinda in a dillema :-/ – Martin Frank Oct 09 '14 at 11:41
  • @MartinFrank in fairness, my wording was "just cut the circle in half" and I hoped people wouldn't be able to misunderstand that ;-) – Joe Oct 09 '14 at 11:56
  • @Joe so simply and yet - you made your bet without me ^^ sorry for maing think complicated, i am glad that you take part in my quest... – Martin Frank Oct 09 '14 at 12:00
  • Nice puzzle. I bet the answer is some kind of fractal. Any mathematician around? – Juan Oct 09 '14 at 14:34
  • The blanket has no shape and size, because it doesn't exist. Try knitting without hands, and you'll see why mama Snake cannot make it. – rumtscho Oct 09 '14 at 20:30
  • 6
    This now has the distinct feel that it belongs on Math.SE, and the "logic puzzle" tag is incorrect. It's just math and geometry – Joe Oct 09 '14 at 21:59
  • @Joe: I agree: Trenin speculated a theory that I think can be tweaked slightly, but neither of us know how to confirm that it covers all situations. – Mooing Duck Oct 09 '14 at 23:53
  • I think a complete solution requires checking (whether analytically or numerically) all one-dimensional, connected curves of unit length which are embedded in R^2. The optimal blanket would be a union of all such curves. Specifically, the union which has minimal area among all possible unions. – do-the-thing-please Oct 10 '14 at 20:18
  • 3
    It's an unsolved mathematical problem. See Wikipedia and Mathoverflow. – sth Oct 10 '14 at 21:06
  • My sister just saw this one. Her solution: Get a small blanket. If the snake changes shape so that the blanket doesn't cover it, punch the snake to make it change into a shape that fits. – mmking Jul 02 '15 at 19:08

17 Answers17

33

As remarked by sth, this is an open problem, a topic of ongoing research. It is known as Moser's worm problem. The Math Overflow thread Smallest area shape that covers all unit length curve cites some recent result.

A known result is that the smallest possible convex blanket has an area between 0.227498 to 0.231999. (In comparison, a half-circle of diameter 1 has an area of about 0.3927.)

Reference: Tirasan Khandhawit, Dimitrios Pagonakis, Sira Sriswasdi. Lower Bound for Convex Hull Area and Universal Cover Problems. Int.J.Comput.Geom.Appl. 23 (2013) 197-212. arXiv:1101.5638. DOI: 10.1142/S0218195913500076. PDF

If the blanket is not required to be convex, smaller blankets may be possible. A special case of interest is if the snake only consists of two straight segments with a bend at a position that may vary, in which case the blanket can be a Kakeya set which can have zero area. It is even true if the snake consists of finitely many straight segments, see the works of Ward and of Davies. For real-analytic curves, the area cannot be zero by a work of Marstrand, however it appears to be not known if it can be arbitrarily small.

Community
  • 1
Gilles 'SO- stop being evil'
  • 3,917
  • 3
  • 23
  • 37
  • Now I know why I can't remember the solution! Oh I wish I had known, and not asked that question here :-$ I really feel bad somehow now :-( – Martin Frank Oct 13 '14 at 04:35
  • 1
    I would like to add that the lower bound quoted is for the problem where the blanket is convex. I am not sure whether existence of a zero-area set has been ruled out. (Indeed, if the baby snake is straight apart from finitely many bends, then answer is zero. It is a basically the famous Kakeya problem.) – Boris Bukh Oct 26 '14 at 00:15
  • @BorisBukh How does a solution based on a Kakeya set work for, say, three segments? Note that the length of the middle segment varies continuously. By the way, this answer is community wiki, feel free to edit it directly. – Gilles 'SO- stop being evil' Oct 26 '14 at 14:21
  • @Gilles. Edit done. ("Basically" meant that with some work one can modify the known constructions of Kakeya sets.) – Boris Bukh Oct 26 '14 at 15:17
  • A zero area blanket? Your kids must love story time. =( – corsiKa Nov 03 '14 at 18:26
15

What about a rectangular blanket that is 1 x circumference of baby snake?

This rectangular blanket could be wrapped around the baby snake (think tube sock) and stretch and fold in any direction with him.

The big bonus here is that mama snake doesn't have to tirelessly keep replacing the blanket, the blanket will go wherever baby snake goes. :)

Sean Johnson
  • 508
  • 3
  • 4
  • 2
    nice thinking, but the snake lies in it's bed and should be covered by that blanket (not wrapped) :/ but i'm sure that would be a really nice baby snake in that tube =) – Martin Frank Oct 09 '14 at 11:43
  • 2
    I don't understand why the obviously wrong answer gets this many upvotes. – Moyli Oct 10 '14 at 06:32
  • 6
    Who said is wrong? I think is the best solution. When the baby bends you just bend the blanket to the same shape... – algiogia Oct 10 '14 at 08:14
  • 9
    @algiogia It is wrong because the problem specifically has to be solved in 2D, and this answer involves a Z-axis. – Kheldar Oct 10 '14 at 12:15
  • 4
    It got so many votes becasue it is thinking outside the box. Almost literally in that it solves the 2D problem in 3D – Frames Catherine White Oct 10 '14 at 23:26
  • @Oxinabox But not literally as a box is 3-dimentional. – bjb568 Oct 12 '14 at 02:51
15

EDIT: After some reflection and help/counter-examples seen in some other answers, I think this is either very close to, or is the correct answer.

What about half of a square with a diagonal of $1$, cut along the diagonal?

For example:

Square Diagonal

Using one of the triangles as the blanket, the long side (i.e. the diagonal of the square) is of length $1$, and the other two sides are length $\sqrt{\frac{1}{2}}$.

The area of this is $\frac{(\sqrt{\frac{1}{2}})^2}{2}=\frac{1}{4}$, and I think all shapes of snakes would fit in it.

Some common snake shapes that will fit:

  • A square of side length $\tfrac{1}{4}$
  • A circle
  • A "U" shape (easy to prove if it is symmetrical, and if it is not symmetrical, then it is covered by a smaller area)
    • e.g. where all three sides are length $\frac{1}{3}$
  • An "S" shape - head goes left 90 degrees, tail goes right 90 degrees

As pointed out by Mooing Duck, if you orient this triangle with its long edge down as follows: enter image description here

then its height is $\tfrac{1}{2}$, but you don't need all that height. The tallest shape the snake can make is when it forms 2 sides of an equilateral triangle. So, if we crop off that portion of the triangle, we end up with a truncated triangle (looks similar to the half hexagon in DenDenDo's answer!). It looks like follows: enter image description here

Its area is now $\tfrac{1}{4}$ minus the amount we just removed. The height of an equilateral triangle of side length $\tfrac{1}{2}$ is $0.433$ ($\sqrt{\tfrac{1}{2}^2-\tfrac{1}{4}^2}$), so the triangle we just removed has height $0.067$. The area of that triangle is $0.0045$.

Thus the area of the remaining blanket is ~ $0.2455127...$

EDIT:

After some more reflection, I wonder if this shape needs to be so symmetrical. You can always flip the blanket over. For example, the left side of the above blanket can cover a snake bent into 2 sides of an equilateral triangle, but the right side isn't used. If you make a "U" shape from the snake with the sides of length $\frac{1}{3}$, then you only need a portion of the right side.

For example, the following blanket still covers both shapes: enter image description here

But the upper right portion doesn't seem necessary. Can it be simply removed? Here is the shape again with some other snakes covered by it.
enter image description here

NOTE: Does the blue equilateral snake need to be oriented that direction? If we orient it so that the missing third line is on the right, can we recover some of the blanket?

Likewise, the brown "U" shape could have the opening facing up, so we could recover some of the interior of the "U".

Also, the green snake is $3$ segments each of length $\frac{1}{3}$. If the middle segment is longer, then the overall shape isn't as tall. If the middle segment is shorter, then it also begins to get shorter, so this one is the tallest of these types, so they will never use the space above the brown "U".

Trenin
  • 8,964
  • 21
  • 53
  • 1
    What does "half a square with a diagonal of 1" mean exactly? I can't think of an interpretation with an area of 1/4 that also covers a snake in a straight line. – Mooing Duck Oct 09 '14 at 23:08
  • 2
    @MooingDuck His "half of a square with diagonal 1" is a "right isosceles triangle with hypotenuse of length 1". – Alexander Oct 10 '14 at 07:43
  • I agree with the triangle idea. If the snake bends, any bend will reduce it's length by at least twice the length of the side protrusion, so you can move the baby away from the longest border and he's still covered – algiogia Oct 10 '14 at 08:11
  • 2
    you say the two sides are $\tfrac{1}{2}$ but they are actually $\sqrt{\tfrac{1}{2}}$ – Ivo Oct 10 '14 at 13:23
  • @IvoBeckers Yes - thanks for that! Think it is right now... – Trenin Oct 10 '14 at 14:06
  • I checked, this case does indeed cover the 0.333x0.333 "square" shape, and the perfect circle. Now I think this general shape is best. – Mooing Duck Oct 10 '14 at 16:37
  • 2
    How does your triangle cover a snake like this, with three segments and angles close to 180 degrees? – Lopsy Oct 10 '14 at 18:58
  • @Lobsy, 180 degrees is a straight line. I think you mean maybe 5 bends? 3 horizontal stretches separated by 2 vertical pieces? In general, any portion not contributing to the length makes it shorter, so it should fit at the bottom of the triangle. That being said, I think that if you look closely at my diagram, the red and black ones leak out of the box. I thought this was an artefact of how I drew them, but mathematically, I see that they don't quite fit. They are very very close though - only off by 0.01, so perhaps I just need to make one side a little bigger. – Trenin Oct 10 '14 at 19:06
  • The equilateral triangle doesn't need to be oriented that way, but any other orientation that does not go below the bottom of the blanket must be taller than the trapezoid we came up with, so it will go above the top and protrude from the blanket. Something to consider is that some n-gons (definitely 5, 6 and 7, I checked) will partly fill the space above the square and left of the triangle (or right, if you prefer). So we can't completely eliminate that area. You are right, the trapezoid is (probably) not minimal. – do-the-thing-please Oct 10 '14 at 20:13
  • @Trenin Lopsy is right. A "long S" snake with 3 equal segments and angles close to 180°, i.e. 170° and 190° won't fit in your shape. Also with angles 120° and 240° you won't find even a close fit. – Florian F Oct 12 '14 at 19:57
  • @FlorianF: I see a snake with 2 bends each of ~20 degrees. Can you explain the 180/120/240 numbers you two are quoting? Trenin and I are confused. – Mooing Duck Oct 13 '14 at 23:19
  • Same as for other post: http://florian.net/puzzle/pic/SnakeEscape.png – Florian F Oct 14 '14 at 21:50
12

Examining all of the answers leads to interesting insights, but my intuition is now telling me that there isn't (an obvious) closed-form solution to this puzzle.

My best attempt at a solution is the union of all line segments of length 1/2 whose endpoints touch each of the x-axis and y-axis simultaneously, and are mirrored over the y-axis. This would look like Trenin's "square-minus-quarter-circle-mirrored" answer. I am fairly sure they are the same shape, but I lack proof.

Unfortunately this solution must be incomplete. Consider if the baby looped itself into any ellipse of unit perimeter--or worse: an ellipse with a break in it. For simplicity* consider a circle. The diameter of such a circle is 1/pi. It turns out a circle of such diameter is too large to fit into the shape described by my answer.

I've used MATLAB to whip up a figure of what I mean by the above descriptions:

enter image description here

Additionally, the solution could be truncated per Mooing Duck's comment on Trenin's answer, and possibly truncated further depending on the number of bends--triangles aren't the only possible bend configuration.

*As a side note, I'll point out that determining the ratio of the radii of ellipses of constant perimeter, given the length of one radius, is quite complicated, involving the inverse complete elliptic integral of the second kind. I found a journal article and related Fortran code for the inverse if anyone is interested (links below now, thanks for the upvotes!). To prove a solution is minimal would require checking every ellipse of unit perimeter, since the circle doesn't fit. This is why I don't think there is a closed-form solution to this problem. Unfortunately both determining a minimum blanket and proving that it is minimal are beyond the time I'm willing to devote to the problem, but may be the subject of a publishable journal article for an ambitious sort.

Edit: Link to article

Link to code used by author of article, as text file

do-the-thing-please
  • 439
  • 3
  • 9
9

I am posting a new answer, building from Trevin's trapezoid answer. I drew a diagram of the answer using Creo (which has some handy-dandy constraint mechanisms built in). Creo is a CAD tool which has a constraint-and-dimension-based sketcher, which is what I am using here. Solid yellow lines are outlines of the sketch itself, and dotted lines are construction lines. Construction lines are not part of the actual part being sketched, but allow for additional constraints to be made on the sketch. Solid blue lines are dimension leaders which tell the dimension of some feature, solid red lines are locked dimensions (so I don't mess up the sketch accidentally by clicking and dragging something). Some aren't locked because they are parameterized using mathematical relationships, as with the circle diameter, which is set equal to 1/pi. Filled yellow areas are considered solid two-dimensions sketch regions, and can be used to make three-dimensional features from. Here they are used for denoting the blanket.

original answer

If we consider a square inside the triangle of side-length 1/2, this actually takes care of the circle problem as well, and can improve the trapezoid's area.

square encompassing unit circumference circle

The square is the highest a quadrilateral of perimeter 4/3 can be (4/3 = 1 for snake + 1/3 for break). If it goes taller, turn it on its side and should still fit. If we drop the height of the square, then the two vertical sides will angle outwards. If we keep doing that, eventually it will become a straight line of length 1. If instead we increase the length of the top, then the other two sides must get shorter. Either way it will fit inside of a 45-45-90 triangle of base length 1. If we trim the sides down we get:

trimmed triangle

I am fairly sure that this area is minimal for all quadrilaterals the snake can take the shape of. As a heuristic argument, I ran MATLAB code for many symmetric quadrilaterals and they converge to a 45-45-90 triangle. It can't be seen in the figure and I am hesitant to make this answer bulkier, but each stair-step is for a different iteration of the length of the vertical legs. Then they are iterated over angle between vertical and horizontal. More iterations looks more like a 45-45-90 triangle. If we trim off the top to account for turning tall quads on their sides, then we get the solution in my third image.

matlab triangle

This solution does not consider pentagons or higher-order polygons in general. It turns out if you put a pentagon with one edge along the bottom, it sticks out into the region between the square and the equilateral triangle just a bit. Hexagons and heptagons do as well. However, none of them take up the entire space there. I outlined the regions that are likely to be improved upon in some way (outline in yellow, see first paragraph):

can_be_improved

Height is sqrt(3)/4, base is 1, top is ( 1 - 2 * ( sqrt(3)/4 ) ). Multiply height by average of bases. The area of the 45 degree trapezoid I came up with is thus about 0.2455 square units.

do-the-thing-please
  • 439
  • 3
  • 9
  • You might mention that the "likely to be improved areas" are highlighted yellow. (As opposed to the bright blue and red lines) Otherwise this answer is incredible. – Mooing Duck Oct 10 '14 at 16:42
  • Thank you for the suggestion (and compliment!), which I've edited in. I am a math and engineering person in academia so I sometimes take details for granted. My apologies for any confusion! – do-the-thing-please Oct 10 '14 at 17:06
  • I agree you in the height of sqrt(3)/4 and the 45° angles on the sides. You probably can cut some of the yellow area. But Where would you place the snake: straight 1/3, turn 60° left, straight 1/3, 60° right, straight 1/3? I think "long S" shapes are still a problem. – Florian F Oct 11 '14 at 16:50
  • @FlorianF: both ends of the snake on the bottom edge, centered horizontally. His "height" is only 0.259 in the middle 0.33333 of the blanket, which has a height of 0.33333, so he fits with lots of room to spare. – Mooing Duck Oct 13 '14 at 23:12
  • Rereading this answer, it dawns on me that it's very close to one of the first answers: a right-triangle with a hypotenuse of 1. We trimmed of that one corner, but it's interesting that that early easy answer was so close! – Mooing Duck Oct 13 '14 at 23:15
  • 1
    @MooingDuck Unfortunately reading the comment by user sth on the question indicates that the problem is currently unsolved and quite difficult. Link: Wikipedia. It was fun building on each others answers and comments though, even if it is unlikely we will come up with "the" solution. – do-the-thing-please Oct 13 '14 at 23:48
  • @MooingDuck: I am speaking of an S shape. If both ends are on the bottom edge, half of the S is below the line. – Florian F Oct 14 '14 at 07:46
  • @FlorianF: in that case, he "starts" in the bottom right corner, and the second bend touches the bottom edge. In this case the "end" touches the horizontal center line with a height of 0.288, so again, he fits in far less than half the total space. – Mooing Duck Oct 14 '14 at 16:50
  • I really don't know how you can end on the center line. http://florian.net/puzzle/pic/SnakeEscape.png – Florian F Oct 14 '14 at 20:21
6

Half-Hexagon, area <= sqrt(3)*3/16 = 0.3927

I think the optimal shape is either a half hexagon or something slightly smaller.
Assume the head of the snake is fixed and it extends to the right along the x-axis, otherwise we just rotate it.

If the snake bends, we can assume the first bend goes up, otherwise we mirror the snake (or flip the blanket over). In worst case it bends in the middle and once it bends sharper than an equilateral triangle, we can align the long side of the triangle on the x-axis and the snake is covered again. if there is only one bend, we can get away with an even smaller droplet-shaped area which is the envelope of several triangles

If the snake bends more often it will only get shorter, which makes it even easier to cover. Again we align the longest side of the bounding polygon on the x-axis and the snake is covered. It needs more area than the shape from before, but still slightly less than a full half-hexagon.

The proof to this is pure intuition and playing around with different shapes in Inkscape

enter image description here

Edit: In the first picture the snake is simply straight.
In the second it can bend once, so it goes half the distance to the right and then in any direction. On the left are the required blankets (partially hiding each other) on the right they are rotated to fit in less then a half-circle.
Same thing with three segments of length 1/3

This is the hexagon I mean, with all helper circles and shadings removed
enter image description here

DenDenDo
  • 219
  • 1
  • 2
  • You haven't specified the size of the hexagon. You need the long side to be $1$ to take care of a straight worm, so let's assume that. I can still take a segment of length $1$ and make two perturbations near one end, one up ad one down, and it wont fit, so at one end the shape has to meet the line at $90$ degrees. – Ross Millikan Oct 10 '14 at 03:21
  • 1
    @Ross but by bending it you make it shorter, so you dont need to put the corner of the shape into the corner of the hexagon. By bending the endpoints of length $x$ by 90° you get a bounding parallelogram with longest side $L(x)=\sqrt{(1-2x)^2+x^2}$, angle $\phi(x) = \arctan(\frac{x}{1-2x})$ and height $h(x) = x \sin(\phi (x))$. Now we need to make sure that $L(x) < W(h(x)) = 1-\frac{h(x)}{\sqrt{3}}$ where $W(h)$ is the width of the hexagon at the distance $h$ from the baseline. The equations are ugly but in a plot it is obvious that it holds true for all x – DenDenDo Oct 10 '14 at 09:17
  • @DenDenDo I think Ross's snake will fit in the 1/2 hexagon. But you'll have trouble with the almost flat S shape: 3 equal segments with an angle 180-epsilon and 180+epsilon. The angle will shorten the snake by a length O(epsion^2) but it will stray away from the axis to a distance O(epsilon) on both sides. So for a small enough epsilon you will have to place it so close to the long edge that it overlaps. – Florian F Oct 11 '14 at 20:58
5

I'm not math-y enough to even begin to go about proving this, but just based on logic I believe you can just cut the circle in half to give you a semicircle with a diameter of $1$ unit, which would have an area of $\tfrac{1}{8} \pi$ (a circle with a diameter of $1$ has an area of ${\pi \cdot\tfrac{1}{2}}^2 = \tfrac{1}{4}\pi$).

This will fit the longest possible layout along the diameter, and I don't think it should be possible for the snake to lie in such a way as to break out of the semicircle.

If anyone can provide any kind of proof (or disproof), feel free to edit my post.

Here's an illustration of the blanket, provided by @MartinFrank. The red lines indicate possible snake positions.

enter image description here

SQB
  • 5,118
  • 31
  • 58
Joe
  • 5,745
  • 1
  • 28
  • 51
4

EDIT: As pointed out by Falco and Ivo Becker in the comments, there are some shapes that do not fit. I will leave this answer here, however, since there is valuable info in the comments. Also, thanks to Mooing Duck for the pictures - better than the one I put up.

I have another thought.

What if you started with a unit square blanket and took away the unit circle from the middle, and then took one quarter of that, you'd have kind of a right-angle triangle, but its long side would be caved in. Now say you mirror this triangle along one of its short edges, and it would be like a bigger right angle triangle, except its two short edges are caved in while its long edge is straight. (Blanket is the red area) enter image description here

Would all snake positions be covered by this blanket?

EDIT: As pointed out by Falco and Ivo Becker in the comments, there are some shapes that do not fit.

Mooing Duck
  • 103
  • 5
Trenin
  • 8,964
  • 21
  • 53
  • fascinating shape, though I had to read this several times to get it. I think it covers all snake shapes, but I can't be certain. Area is... ~0.1073009? – Mooing Duck Oct 09 '14 at 23:13
  • The more I think on it and read the other answers, the more I think you hit the right shape. I made a diagram here, blanket is the red part: http://i.imgur.com/eZ5Ai3P.png The key is that the snake's head is only at the Left/Right corners if he's perfectly straight, otherwise the bend is towards the top. Or maybe it needs to be a perfect triangle like your other answer says... I can't tell. – Mooing Duck Oct 09 '14 at 23:23
  • Aha, a clearer way to think of it is that both ends of the snake are almost always on the long flat side (assuming 0-1 bends. For more bends you can more-or-less center the snake) – Mooing Duck Oct 09 '14 at 23:33
  • After thinking on it a while, I am now 100% convinced this covers all snake positions with a single bend in the exact middle. But the more I think about it, if the snake is in an equilateral triangle with the long edge, and continues bending, the blanket can be spun, so that additional height is definitely unnecessary. – Mooing Duck Oct 10 '14 at 00:02
  • As shown here: http://i.imgur.com/8LqDJZC.png – Mooing Duck Oct 10 '14 at 00:09
  • no.... even more can be cut out. If the snake in the equatorial position is rotated so that one of his edges lays along the long edge of the blanket, it becomes obvious that even more can be trimmed. I'm not sure of the shape though :( – Mooing Duck Oct 10 '14 at 00:11
  • 2
    I think this will not work, if the snake tilts its head right and tail left (so a 0.9 straight line, with 0.05 rectangular bit at each end, one to the left, one to the right) – Falco Oct 10 '14 at 08:30
  • 1
    Also, when the snake is rolled up like a square (with sides 0.25) it won't fit I think – Ivo Oct 10 '14 at 09:23
  • @Mooing Duck - thanks for the picture. Go ahead an update the answer with it, or put it in your own answer. Your analysis is similar to what I did, but I struggled to put it into words. Good job. – Trenin Oct 10 '14 at 11:20
  • @Falco So your counter example is basically like a number 7 with a tail? – Trenin Oct 10 '14 at 11:29
  • @Falco You are right - that shape does not fit. – Trenin Oct 10 '14 at 11:30
  • @IvoBeckers Nice counter example - that too does not fit. – Trenin Oct 10 '14 at 11:44
  • @MooingDuck Thanks for the pictures. Falco and IvoBecker found counter examples though. In fact, I think that a snake like the number 7 (a 90 degree bend, but not in the middle) would prove un-coverable by this blanket. – Trenin Oct 10 '14 at 11:52
  • @Trenin: I think that a number 7 would fit, with both ends of the snake along the long side. I don't know how to prove it though. Will see if I can figure out how to test the .25 side square, that's a good counter-argument. (Nevermind, starrise showed that this solution doesn't cover the perfect circle case. I really thought it would. – Mooing Duck Oct 10 '14 at 16:24
  • 1
    @MooingDuck An even bigger "square" is the "U" shape with 1/3 on each side. That one won't fit. As for the "7", It is not that much shorter than the snake when it is straight, but now it must be elevated - the length of the maximum allowed long piece shrinks more rapidly than the short side grows, so it doesn't fit either. I cut the pieces out of paper, and it is not even close to fitting. – Trenin Oct 10 '14 at 16:29
3

Looking at Joe's answer, half the semicircle seems to be unnecessarily big. Instead, you could use a smaller area triangle of the same height and width.

If you were to take a semicircle of diameter 1 and split it in half, replacing one side with a triangle of height 0.5 and width 0.5, I think that would be the smallest area.

Area: Half the semi-circle + triangle

Circle area: pi * r^2 = pi * (1/2)^2 = pi/4

Half the semi-circle = pi/4 * 1/2 * 1/2 = pi/16

Triangle area: length * height / 2 = 1/2 * 1/2 * 1/2 = 1/8

Total area: = pi*/16 + 1/8 ~= 0.32

Trenin
  • 8,964
  • 21
  • 53
  • I think it can be reduced to a right-triangle with a base of 1 and a height of 0.5. Actually, it probably doesn't even need that much height. – Mooing Duck Oct 09 '14 at 23:28
  • I think the most height required is when he forms a equilateral triangle with the long edge, so... a height of 0.433012 using an area of... ~0.21650635. The more I think on it, the more I think even this has wasted cloth, but not much. I think you're very very close. – Mooing Duck Oct 09 '14 at 23:31
  • @MooingDuck Yeah - this was my first attempt. My other answer was just a simple right angle triangle (area 0.25), and my third was the funny dented triangle (which doesn't work). I've never posted more than one answer before, but I kept getting better ideas and didn't want to delete them, since they all had valid points... – Trenin Oct 10 '14 at 12:00
3

A blanket the same width and length of the snake would seem to be sufficient. Blankets are soft, and bend just like snakes can bend - depending upon theur construction, they may be able to bend more. In this case, let's assume a knit blanket, loose enough that it can stretch to bend just as much as the baby stretches to bend, without having to be folded over or bunched up. This has the nice effect of keeping the problem 2 dimensional. . Mommy snake can adjust the blanket at any time so that it bends to cover baby snake

atk
  • 132
  • 4
  • It's sufficient, but it can be made smaller. –  Oct 10 '14 at 23:31
  • @JoeZ, how can you cover an object with a smaller area than the object? – atk Oct 10 '14 at 23:32
  • Well, you don't need a rectangle the length and width of the snake, as some of the other solutions have shown. –  Oct 10 '14 at 23:34
  • All the other solutions are larger than the snake... they try to address the snake's movement without bending the blanket. I take the opposite approack. If the snake is 1x0.001, then the blanket is 1x0.001. No empty space under my blanket, but empty space under everyone else's – atk Oct 10 '14 at 23:36
3

Assuming the line (snake) has a negligible width, this shape (blanket) will contain every possible bent/zig-zagging of a 1-unit line, assuming the shape can be rotated in three dimensions:

enter image description here

The total area adds up to a quadrant of a 1-unit square. More specifically, ¼u² or 0.25 units squared.

Regarding the area, it cannot get any smaller because the largest bounding box for all possible bents has that specific area - it's the 90-degree mid-way bent.

Rand al'Thor
  • 116,845
  • 28
  • 322
  • 627
Vercas
  • 131
  • 3
  • Can you prove that it will always cover the snake and can't get any smaller? – Ben Aaronson Oct 10 '14 at 17:49
  • I could simulate a few hundreds to tens of thousands of bends and fill in a matrix. Would that suffice? – Vercas Oct 10 '14 at 18:00
  • I guess. but you must have come up with this solution based on something. Even if you can't prove it rigorously, it'd be good to know your reasoning – Ben Aaronson Oct 10 '14 at 18:02
  • @BenAaronson Darn, only the arc was supposed to have 1/4. I used the wrong character. Imma fix it. Edit: Fixed. Also, I came up with this when simulating bents in my head. I place a lot of trust in my head. – Vercas Oct 10 '14 at 19:27
  • Can you explain your reasoning behind 0.25 being the smallest possible area? – Mr.Mindor Oct 10 '14 at 21:34
  • 4
    How would you place a snake that is straight except for 1% bent at 90° at both ends? – Florian F Oct 10 '14 at 23:01
  • @FlorianF One end being on the bottom of the shape in the picture, it can be offset enough to fit the other end in the top arc. – Vercas Oct 11 '14 at 10:59
  • @Mr.Mindor Taking a line bent at 90 degrees mid-way, you can add an infinite amount of bends at any point. 90-degree bents yield the largest surface area and so they are the only ones which need to be accounted for. This process will plot the bottom curve, considering that you can rotate/flip this shape. For very fine and subtle bents, like the one Florian F mentioned, the top curve exists. – Vercas Oct 11 '14 at 11:14
  • 2
    @Vercas I don't think it fits. The top end is still at 0.02 units from the top. At that place the shape is only 0.0004 units wide. – Florian F Oct 11 '14 at 16:21
  • @FlorianF Draw this on a large sheet of paper and draw a line like you described. I'd do that but I've absolutely no paper in my room and the hall administration wouldn't be happy if they catch me drawing on the walls. – Vercas Oct 11 '14 at 16:44
  • 1
    @Vercas You can calculate it. 0.5 - sqrt(0.5^2-0.02^2) = 0.00040016. I am assuming your figure has 2 perfect 1/4 circles. – Florian F Oct 11 '14 at 20:41
2

I'm not seeing this one here yet.

a 30-60-90 triangle with sides 1/2, sqrt(3)/2, and 1. Total area =0.2165

I believe this shape allows for all single bends of the snake. triangle layout

For bends between 0 and 60 degrees, the bend should be placed in corner A: placement for bends 0 to 60 degrees

For bends greater than 60 degrees, one end should be placed at Point A:enter image description here

Further analysis is required for additional bends.

Mr.Mindor
  • 221
  • 1
  • 5
  • It might work for 1 bend. It doesn't really tell how it works if the bend is not in the middle. But with 2 bends, some won't fit. – Florian F Oct 11 '14 at 16:23
1

Stretch your 2D baby snake out so that it forms a straight line from nose to tale. Find the 2D silhouette that the baby now forms. Create a 2D blanket having the same shape as the silhouette. Spread glue on the blanket and attach it to the baby snake. Mama's 2D baby snake will always be covered in bed once the glue dries.

  • The blanket will have minimal size.
  • The 2D blanket will twist and stretch and turn with the 2D snake it is attached to.
  • The size of the blanket will be the area of the baby's silhouette.
  • The form or shape of the blanket will always conform to the baby's.
  • The length of the blanket will obviously be 1.
  • The 2D blanket will always take the same shape as the baby.
  • The blanket will always cover the snake since they are glued together.
  • Mama will not have to worry about the baby being covered since both are deformable.
Noctis Skytower
  • 451
  • 5
  • 21
  • that is an really good approach, i never though of this! solving the problem in 3D might really lead to an proper solution ^^ (although the snake-puzzle is supposed to be an 2D-Problem) – Martin Frank Jul 02 '15 at 05:02
1

The blanket is a circle with a diameter of 1. There is no position the baby snake can take which this blanket cannot cover. (Unless the snake's width is greater than 1; this wasn't specified, but I'm hoping it's a safe assumption.)

Miniman
  • 550
  • 5
  • 13
  • i've posted your answer into my question - i think there are lot's of areas that can be clipped. I'm looking for a smaller solution! but thank you for providing this answer! good thinking and a good start!! – Martin Frank Oct 09 '14 at 04:42
  • 5
    It's trivial to show that this is not the minimal solution. Just clip a small piece off one end, say 0.1 units. If the snake bends so that its maximum length is 0.9, it can fit anywhere under the blanket. If it's longer than 0.9, the blanket can be rotated so that it fits under the uncut part. – Moyli Oct 09 '14 at 07:13
  • 1
    @Moyli yes, you are right... don't be to harsh, i think that is still a agood start of thinking... honestly i think this is a quite very hard puzzle... – Martin Frank Oct 09 '14 at 07:43
  • but still is has funny snakes ^^ – Martin Frank Oct 09 '14 at 07:43
1

I think the best solution is a 1*1/2 rectangular blanket. If the baby is stretched out, you can cover him entirely. if he's in a non-stretched out pose, there cannot be more than 1 part sticking out further than 1/2 from the rest of the body.

edit: to reply to the remark: instead of a rectangle with size 1*1/2, use a rectangle with diagonal length 1, height 0.894 and width 0.447.

Nzall
  • 995
  • 5
  • 24
  • 3
    It would be bigger than Joe's semicircle blanket and it would have way too much extra space. For example the snake could never touch the opposite corners of the rectangle which shows the blanket is too big to be an optimal solution. – Moyli Oct 09 '14 at 11:10
  • 2
    A rectangle with diagonal length of 1 and what would the other dimensions be? If the height would still be 0.5, it would still be bigger than a semicircle (0.43 sq vs 0.39 sq). – Moyli Oct 09 '14 at 11:34
  • @MartinFrank yes it is, just put it at an angle so that the corner is aiming towards the long side. – Nzall Oct 09 '14 at 11:47
  • ...with those measurements it's still larger than a semicircle (0.40 vs 0.39). – Moyli Oct 09 '14 at 11:55
  • if the snake would make a U (semicircle, circumfence=2, radius = 1/pi = 0.32) it would not fit under the blanket... take your diagnal line, go 0.3 into center, then make a turn of 90° and go again 0.3 units - you are outside then (freaky, i must now use my circle/compass) – Martin Frank Oct 09 '14 at 11:58
  • i hope i didn't measure wrong but when i draw it on my sheet it doesn't match! – Martin Frank Oct 09 '14 at 11:59
  • @MartinFrank the easier method is not to draw it, but to cut out a figure that you want and overlay it over an .894x.447 rectangle. – Nzall Oct 09 '14 at 12:00
  • @Moyli You can cut off part of 2 opposite corners, as long as you do not reduce the minimal distance between opposite sides too much. I'm currently working out how much that should be. Then again, you can also squish the semicircle to remove excess line length. – Nzall Oct 09 '14 at 12:02
  • @NateKerkhofs I think if you cut 2 triangles off, you'll get my solution. Is it enough to cover the snake in all configurations? – Trenin Oct 09 '14 at 17:33
  • You cannot cover a "nunchaku" snake having 3 segments of length 1/4,1/2,1/4 and 90° bends. – Florian F Oct 10 '14 at 23:29
1

The correct answer has already been given

The SemiCircle covers everything:

First, we need to cover the full length of the snake - a line with length 1:

enter image description here

Then we need to ensure to cover - as outlined above - any angle between 0 and 180°. Worst Case: it's exactly a 50:50 split -> Thales circle:

enter image description here

This case covers everything, including the snake forming a circle itself:

enter image description here

Whatever "shapes" the snake will perform on any of the both tails (if splitting at 50%) it will NEVER have a absolute length of 0.5 therefore remaining IN the semicircle all the time.

Any solution having a streight line, but lesser area will not work, because the snake could be like v-------------------^, messing up any attempt to have a line involved just to cover the maximum length

dognose
  • 119
  • 3
  • I think this is the "semicircle big" that is mentioned below as being a valid- but probably not minimal- solution. I don't really understand the small semicircle myself... it's pretty trivial to see that any semicircle with diameter less than one couldn't fit a snake that was stretched completely straight, so I don't know why that much more complex diagram was included – Ben Aaronson Oct 11 '14 at 15:31
  • Well, if this is referred as semicircle big then it's the minimalisitc solution, because it needs to cover all the angles between 0 and 180°. NOTHING in the shape but the baseline could cover the snake at a streight line and every point on the circle is required per degree the snake could form. So that's minimalistic. – dognose Oct 11 '14 at 15:37
  • 2
    Not sure I buy that. For example, take any of the angles formed by the baby in your second picture. The mama snake could move the baby to the right a bit, and now he wouldn't be touching the curved edge. And with that in mind, if you point to a given part of the curved edge, I don't think it's at all clear that the mama snake couldn't get by if a little chunk was cut out of that part of the edge (with a few exceptions at certain spots) – Ben Aaronson Oct 11 '14 at 15:53
-2

well i'm not sure if i really have a valid answer, but so least blanket i could think of is shape a little weird...

enter image description here

you can put into that blanket

  • the streched snake,
  • the 90°L-baby snake,
  • the U-Shaped baby snake,
  • a snake shaped like a [___] (dunno how to call that, is bend on tail and head)...
  • a S-shaped snake would also fit in...

im not sure if I could bring in a Z-shaped baby snake if it had 2x 60° bends...

but what's worse: What is the size of this shape? I can't tell and therefor can't compare with others :-/ ... frustation ... if anyone knows sie size fo such an area let me know...

Martin Frank
  • 731
  • 7
  • 14