What is correct answer for this IQ task and why?
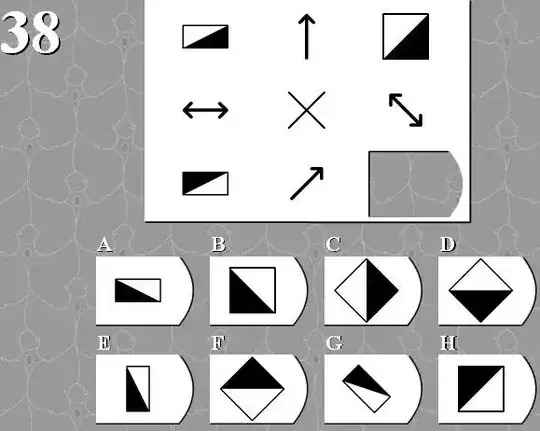
What is correct answer for this IQ task and why?

The answer is:
F
I googled and found the test this task is taken from: http://www.iqtest.dk/testEnglish.swf
If I answer 1-10 questions correctly and 38 H, I get IQ 92.
If I answer 1-10 questions correctly and 38 F, I get IQ 93.
So I conclude that correct answer is F.
How I understand this puzzle:
In the corners (cells: 11,13,31,33) we have some objects. In the middle edges (12,21,23,32) we have operators on neighbouring two objects. The centre cell (22) is simply do not used here [this opinion agrees with tasks 4 and 9 at the same test, where it is used similarly].
Let's look on (12) operator (one arrow), it leads to simple vertical stretching of object.
Let's look on (21) operator (two arrows), it leads to simple swap of object colours.
Now we are looking on (23) and (32). (23), by our assumption, should swap colours of (13), creating the object from varian H, plus some additional operation, since (23) is different from (13). (32), by our assumption, should stretch (31), making variant H from it, plus some additional operation.
What are these additional operations? Since they make the same object from the same object (H) that must be the same. Looking on possible answers we see that all differences between objects are: size, swap of the colours, angle. We have notations for first two differences, so additional operation should be rotation.
We see that (23) is rotated respectively to (21), by 45 degree clockwise. (32) is rotated respectively to (12) by 45 degree clockwise. So most probably both additional operations means rotation by 45 degree clockwise. This means that the right variant for (33) is F.
What I do not like about this solution:
I hope, someone else will find even better explanation, without mentioned two drawbacks.
H.
Various categories of symbol appear on alternate rows and columns:
Odd row, odd column - rectangles shaded in two colours, with diagonal dividing line. Odd row, even column - single headed arrows Even row, odd column - double headed arrows Even row, even column - cross
Each category of symbol appears to have its own type of transformation:
Odd row, odd column - height increases moving right, which half is shaded swaps moving down (or 180 degree rotation moving down) Odd row, even column - 45 degree rotation clockwise moving down Even row, odd column - 45 degree rotation clockwise moving right Even row, even column - ? (only one member)
In the absence of any obvious common rule for all symbols, I conclude that each set follows its own rules. Thus the answer is H (column 3 = tall, row 3 = top left half black).
I did wonder if the arrows represented transformations for the squares on either side - the arrow in row 1 column 2 could represent a height increase. The double headed arrows suggest a flip to me but would have to represent a rotation for this to work. But this system breaks down with row 3 column 2 - there are no answers which have been stretched along a diagonal (which would give a parallelogram).
Like bmj, I also get H as the answer. However, my logic is much more straightforward:
We see:
Therefore:
Resulting in a color-inverted square.
The arrows and $\times$ are just distractions.
The answer is
F
Though I get it slightly differently. I got this answer before looking at the other answers, just in an attempt to solve it myself.
The first thing I noticed is that the arrows are different lengths. The exact length of the arrow is also the exact size of the shape it is referring to.
For example, the one at the top stretches the box to exactly that length.
I also came to the conclusion that a double arrow means to flip colors.
I realized that the [2,1] arrow did not change the size of the box only the colors, this does not mean that the double arrow ONLY changes colors though, it just means it ALSO changes colors. The arrow length is the exact size as the box in [1,1] and in [3,1], which means the size didn't need to change from that arrow.
However, since the box at [3,1] stayed the same size we can assume that the arrow at [2,1] only effects the horizontal lines (aka the top and the bottom lines). The arrow at [1,2] only effects the vertical lines (aka the lines on the size of the box).
Using this logic of it decided the exact length of the box based on arrows, and that the arrows at [1,2] and [3,2] are effecting the side walls and the arrows as [2,1] and [2,3] are effecting the top and bottom sides. We can assume right away it must be a diamond shape, since that is the length of the arrows and how they are shaped.
After that I just simply replaced the bottom and top of the box at [1,3] with the length of lines from [2,3], then fliped the colors. Then we combined that with the sides of the box of [3,1] being replaced with the arrows from [3,2] and when we combine we indeed get F.
Here is an image I did in paint to show the combining and replacing of sides:
You can see that if you combine those 2 pictures together that is what you end up with.
The most important part I saw that was overlooked was that the arrows were always the exact length and direction of the side of the box that was being effected. This is how I came to the conclusion of the answer for this question.