10

The governor of Reniets (a land far, far away!) is known to be very stingy.
He has to build a road which connects all the five cities in the region, which are oddly arranged on the vertices of a regular pentagon (see the picture below).
Building a road is very expensive: the longer it is, the more it costs!
His first idea is to build five roads, each connecting a city to the center of the pentagon, then he realizes that it might not be optimal. In fact, he remembers that, years ago, his friend had to connect four towers, and the solution wasn't trivial!.

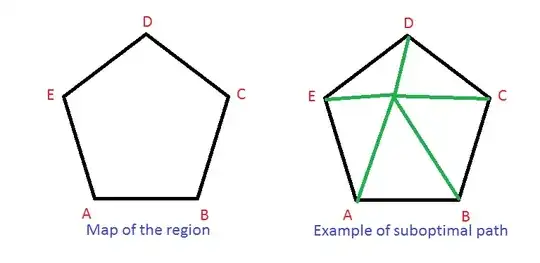
enter image description here

How long is the shortest path that connects all the five cities?

Notes:

  • assume that the side is long $1$ km.
  • I currently don't know the solution, I will accept the most convincing answer if no proof is given after some days.
  • If you can generalize the solution to polygons of any number $n$ of sides, I will award a bounty (the amount depends on the quality of the work).
Community
  • 1
leoll2
  • 12,590
  • 3
  • 39
  • 83
  • 4
    An NP-Complete problem involving involving a open question. Nice light stuff for a Saturday morning! – Bob Jun 13 '15 at 09:02
  • @Bob What's the progress to this? Its evening here :) – Sharad Gautam Jun 13 '15 at 09:08
  • @Bob The actual NP-problem is the generalization to any set of points, not necessarily in a regular pattern. This problem is simply a pentagon, I doubt it is NP-complete; I don't know if it is for regular polygons too, the bounty is for that. Sharad, I've opened a chat room http://chat.stackexchange.com/rooms/24771/leoll2 for all those who want to ask anything about me. – leoll2 Jun 13 '15 at 09:09
  • +1 Cool question. How do you come up with stuff like this? – JLee Jun 13 '15 at 12:08
  • 1
    @JLee Thanks! My original intention was to post the famous square puzzle, but it was already posted by another user, so I decided to add a variation. People seem to appreciate it, I already have few puzzle with similar features ready to be posted in the next days :) – leoll2 Jun 13 '15 at 12:20
  • @leoll2 Meet me now, there – Sharad Gautam Jun 13 '15 at 13:03
  • I once saw a demo where someone made vertical pillars (nails or something) between two transparent plates. They put it on an overhead projector and then added a soap solution to join the pillars with a soap bubble. It's basically an analog computer to calculate the minimum path length. In this case, you'd put 5 pillars. They always ended up with nodes with 3 spokes separated by 120 degrees. You could also make an angle between the plates to add a weighting factor for a variable cost per mile. – Dr Xorile Mar 03 '19 at 22:32

1 Answers1

2

Here's the optimal solution for the pentagon:

enter image description here
As the only Steiner tree for this set of five points, it is the only locally minimal solution, hence it must be globally minimal.

For regular hexagons and above, just take the perimeter and remove one edge.

EDIT: Whoops I forgot to calculate the total path length. Brb.

EDIT2: The length of the tree in the pentagon is $${1\over 2}\sqrt{17+7\sqrt{5}+\sqrt{390+174\sqrt{5}}} \approx 3.891 ~\text{km}.$$ For an $n$-gon ($n \ge 6$) the total path length would obviously be $n-1~\text{km}.$

Anon
  • 2,684
  • 1
  • 12
  • 18