Find the liar in the library

Question

I've just taken a CS exam, which had the following question

6 persons entered a library the day a book got stolen. Each of them entered the library once and only once, and stayed there for some time, then left. If two persons were in the library at the same time, at least one of the two saw the other. After the investigation, the testimonies were

• Albert stated he saw Bernard and Édouard

• Bernard said he saw Albert and Isabelle

• Charlotte said she saw Didier and Isabelle

• Didier said he saw Albert and Isabelle

• Édouard said he saw Bernard and Charlotte

• Isabelle said she saw Charlotte and Édouard

Only the culprit is lying. Who is he/she ?

EDIT: I haven't had the time yet to check everybody's answers and claims.

To those saying the problem is ill-posed, I've actually translated the exact wording from the exam (Question IV.C https://www.concours-centrale-supelec.fr/CentraleSupelec/2015/MP/sujets/2014-033.pdf). As Meelo suggested, this can be solved swiftly with interval graphs.

Answer 1

I think I have an answer:

Didier is lying

I started drawing a graph, eventually gaining this timeline of events (overlaps acceptable).

$Edouard \leftarrow Albert \leftrightarrow Bernard \rightarrow Isabelle \leftrightarrow Charlotte \rightarrow Didier$

You can connect the other sightings, to have at least one relationship,

save for Didier. Didier observes Albert and Isabelle, but there is no relationship between Didier and Bernard, even though they should overlap in some way in order for Didier to observe both Albert and Isabelle. (Didier observed Albert and Isabelle. Bernard is between Albert and Isabelle. Therefore either Bernard should have seen Didier or Didier should have seen Bernard as they would have been at the library at the same time).

Also

Édouard or Didier would have observed the other from their overlapping timelines.

You can verify the answer with this image.

Answer 2

This is perhaps the interval graph solution LeGrandDODOM referred to.

Create a graph by

adding an edge between each pair where one supposedly saw the other.

We then have

If everyone is telling the truth, the resulting graph is an interval graph. Interval graphs clearly cannot have an induced $C_4$, but the resulting graph has at least two: $ADIB$ and $ADCE$. Hence not everyone is telling the truth and the lies must correspond to edges or non-edges to make both of these $C_4$s not induced. Thus $A$ or $D$ is lying as these are the only two on both $C_4$s. $D$ may be lying about seeing $A$, or perhaps $A$ is lying about not seeing $C$ and $I$. As far as I can tell, either case can happen.

Answer 3

Because the problem states that exactly one of them is lying, it must be the case that they were not all in the library at once. If they were all in the library at the same time, each of them would have been able to make their statements truthfully, contradicting the one condition.

Let:
$A$ Albert
$B$ Bernard
$C$ Charlotte
$D$ Didier
$E$ Edouard
$I$ Isabelle

Then:
$A \rightarrow B + E$
$B \rightarrow A + I$
$C \rightarrow D + I$
$D \rightarrow A + I$
$E \rightarrow B + C$
$I \rightarrow C + E$

Now let's expand one step:

$A \rightarrow B + (A + I) + E + (B + C)$
$B \rightarrow A + (B + E) + I + (C + E)$
$C \rightarrow D + (A + I) + I + (C + E)$
$D \rightarrow A + (B + E) + I + (C + E)$
$E \rightarrow B + (B + E) + C + (D + I)$
$I \rightarrow C + (D + I) + E + (B + C)$

Here, we notice that $D$ is the only one that doesn't have someone see him after one step. Let's expand again:

$D \rightarrow A + (B + (A + I) + E + (B + C)) + I + (C + (D + I) + E + (B + C))$

Here is the first chance that $D$ has been mentioned in his graph. Unfortunately for him, the graph also contains all of the other people, which can't be the case (as discussed earlier).

---

Of course, a scenario could be constructed such that $D$ is invisible (by hiding or being quick or whatever). Because there is only one person that claims to see this invisible person, that person is allowed to be the single liar. Any other person is stated to have been seen by at least two people, so everyone else must have actually been seen by at least one person. Our old friend "Invisible Didier", however, cannot be seen by anyone. Hence, Charlotte is a liar and the culprit.

Answer 4

To start: We need to define who was in together at the same time: We'll start off assuming everyone is honest and then look for contradictions.

The relations are as such:

AB, AD, AE, BE, BI, CD, CE, CI, DI, & EI

In all of these cases, at least one person claimed the other was there at the same time.

For the record, the missing relations are:

AC, AI, BC, BD, & DC

So with this information we can figure out who was supposed to be in at the same time. Since AB, AE, & BE are all present at the same time we can conclude that all three were there at (more or less) the same time for the purpose of creating a timeline. All the "combined" relations are:

ABE, AD, BEI, CDI, & CEI

Visually that becomes:

A ---|---|   |   |
B ---|   |---|   |
C    |   |   |---|---
D    |---|   |---|
E ---|   |---|   |---
I    |   |---|---|---

We can now attempt to organize this into a timeline. Since each person only entered once, each line should be intact. This is the best we can get:

A ---|---|   |   |
B    |---|---|   |
C    |   |   |---|---
D ---|   |   |   |---
E    |---|---|---|
I    |   |---|---|---

Ok, so the problem is obvious: We have a cyclical timeline. This timeline only makes sense if we turn it into a cylinder, because no matter how we attempt to put it together (on a straight 2D path) one of the lines is going to be at both ends of the graph without connecting all the way through. So now we can try to verify each of the above relations. We'll go in the order of the "corrected" graph, and we want to rely on cyclical relationships. In other words - 1 sees 2 who sees 3 who sees 1 because that confirms all three are there. Even if, say, 1 was lying, 2 confirms 3 and 3 confirms 1. Since there can only be one liar; 2 confirms themselves by being witness to 3.

AD: D sees A, but A does not see D. No one else is around to complete the circle. Unconfirmed.

ABE: E sees B, B sees A, A sees E (and also B). Confirmed.

BEI: E sees B, B sees I, I sees E. Confirmed.

CEI: C sees I, I sees E, E sees C. Confirmed

CDI: D sees I, I sees C, C sees D (and also I). Confirmed.

Interesting - only one unconfirmed. Also interesting is that we have a double confirmation (where 3 sees both 1 and 2) on either side of the unconfirmed relation.

So one unconfirmed means that that one (AD) has to be the false sighting - and since AD is D's claim - that makes Didier the dirty lying thief.

• Do not pass Go.
• Do not collect $200.
• Give the book back, jeez.

Answer 5

The Problem is ill Posed

If both person 1 states they see person 2 and person 2 states they see person 1 then they must have been in the library at the same time. This is true because at least one of person one and person 3 must be telling the truth as there is only one liar.

To move further we need to further define what it means to lie:

If lying by omission is not lying

In this case people are allowed to have seen people they do not mention without being considered liars. The only way to be considered a liar is to say you saw someone you in fact did not.

If this is the case then:

Any of them could be a liar.

First lets tabulate the statements, if the column header stated they saw the row header then I'll mark that intersection. If it was a corroborated sighting it is marked with an X, if it was a one directional sighting it is marked with a ?

  a b c d e i
a \ X   ?
b X \     ?
c     \   ? X
d     ? \
e ?       \ ?
i   ? X ?   \

From this we can see each person stated at least one uncorroborated sighting.

This means that any of them could be the liar: Everyone except the person the liar supposedly saw arrives. Then the liar leaves and the last person arrives. Now everyone would have seen everyone with the exception of the liar and the person they supposedly saw. Since the person they supposedly saw did not claim to see the liar, they did not lie. Thus everyone except the liar only told lies of omission and any of them could have done it.

If the whole truth and nothing but the truth is required

In this case we can make some more deductions.

If neither person 1 states they see person 2 nor person 2 states they see person 1 then either they must not have been in the library at the same time or one of them is the liar. This is true because if they were in the library at the same time at least one of them would have seen the other so then one of them must have omitted seeing the other and is thus lying.

The liar could have been there the entire time. The liar could just be lying by omission. As long as everyone else's testimonies are consistent this should be valid. This means that any consistent system of testimonies with 5 people could be valid with the 6th person being the liar that was there the whole time. Thus we can just examine each 5 person subsystem. Thus the analysis that follows excludes the liar from the the analysis, and anywhere is says people or person, this means truth telling people/person as the liar is excluded from the analysis.

First lets try the full system assuming no liar:

Assuming no lies then here is a table where an X indicates that the row header and column header were in the library at the same time, and a blank indicates they were never in the library at the same time (top half used only for clarity):

  a b c d e i
a \ X   X X
b   \     X X
c     \ X X X
d       \   X
e         \ X
i           \

Now if pair 1&2, pair 2&3, and pair 1&3, each have an X then 1,2, and 3 must have all been in the library at the same time. We know this must be true because none of them can reenter the library. WLOG 1 arrived first. 1 must not leave until both 2 and 3 have arrived. WLOG 2 arrives next. 2 must not leave until 3 has arrived. Thus when 3 arrives they will all be there.

There are no sets of 4 people where each pair of people has an X. Thus there was not a time when there were 4 people simultaneously in the library. This means that the periods where there were at least 3 people in the library were never interrupted by a forth person coming or going and can be considered one time unit. (Remember the caveat that the liar is excluded, so the liar my be present simultaneously with three truth tellers)

In the 6 person system there are 4 triplets:

ABE, BEI, CDI, and CEI

If these three triplets exist on the timeline then all of the X's involved with them will be satisfied. The remaining X's that need to be satisfied are:

  a b c d e i
a \     X  
b   \
c     \      
d       \
e         \  
i           \

AD. For each of these pairs (just one in this case) there must be a time period during which only the pair is in the library as none of these pairs is part of a triplet.

Thus a list of occupancies that must have existed at some point during the day are as follows: ABE, BEI, CDI, CEI, and AD

This can be visualized in tabular where the rows are people, the columns are time periods and an O indicates occupancy.

  1 2 3 4 5
a O       O
b O O
c     O O
d     O   O
e O O   O
i   O O O

To be a solution the time periods would need to rearrange so that each person occupied the library only during consecutive periods. As expected these periods cannot be arranged in such a manner. Proof for those interested otherwise skip to the next section:

For i's visit to be consecutive periods 2, 3, and 4 must be next to each other. withing that span 2&4 and 3&4 must be consecutive for e and c respectively. That only allows the order 2, 4, 3 or its reverse:

  1 2 4 3 5
a O       O
b O O    
c     O O
d       O O
e O O O
i   O O O

For d to be consecutive 5 must be consecutive with 3, and for e and b to be consecutive 1 must go next to 2, but for a to be consecutive 1 must go next to 5 which is impossible. Thus indeed someone must be lying.

The Possibilities

A lied

Following the same logic as the previous example we can construct tables without A (s A could have been there the whole time if they're lying, This really boils down to removing A from the final period table:

  2 4 3
b O
c   O O
d     O
e O O
i O O O

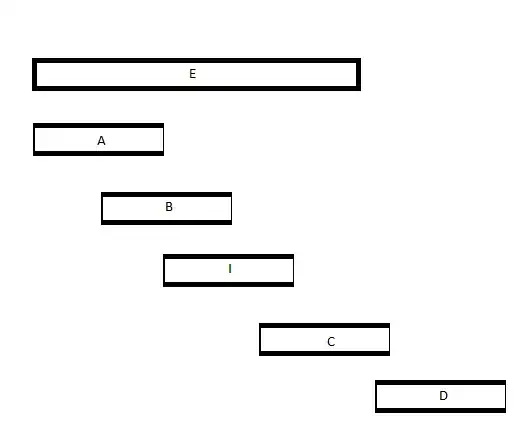
This is a legitimate possibility. A could be the culprit. Here's a diagram of the library occupancy including who saw who when. Note that A did not see B despite saying they did, whereas everyone else saw only who they said they saw, and no two people were in the library at the same time without one of them seeing the other.

B lied

  1 4 3 5
a O     O
c   O O
d     O O
e O O
i   O O

Again not possible

C lied

  1 2 3 5
a O     O
b O O
d     O O
e O O
i   O O

Again not possible

D lied

  1 2 4
a O
b O O
c     O
e O O O
i   O O

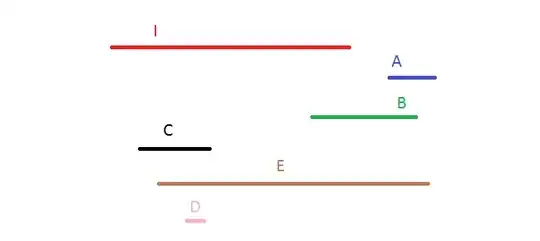
This scenario is also possible so D could be the culprit: Note: that here D said they saw A but they instead saw E. This Solution allows for everyone to see exactly 2 people, which is slightly more in line with the problem statement, so if the problem statement was modified to state that each person saw exactly two people then D would have to be the culprit as if A was the liar they would see a minimum of three people.

E lied

  1 2 3 5
a O     O
b O O
c     O
d     O O
i   O O

Again not possible

I lied

  1 4 3 5
a O     O
b O
c   O O
d     O O
e O O

Again not possible

Conclusion

This problem has two solutions as stated, but could be easily modified to eliminate A as the culprit by stating that each person saw exactly two other people in the library. In that case D is the culprit. Another modification/interpretation that some people took and would result in the same conclusion: The lair included no truth in their statement while the honest students stated the whole truth and nothing but the truth (but this makes the puzzle much easier, and relies on using two different definitions of lying). Yet another modification would be to state that no one, including the liar, saw anyone that they didn't claim to see.

Answer 6

Note: this answer assumes that a truth-teller says ALL the truth, without omitting information.

The symbol $X-$>$Y$ means that $X$ saw $Y$. We know that:
$A-$>$E$
$E-$>$C$
$C-$>$D$
$D-$>$A$
Which means that $A,B,C,D$ were all in the store at a certain moment. Though, there isn't any edge (graph edge, I mean) between $A-C$ and $E-D$, which should be mandatory if they're all telling the truth. Therefore, the liar is $A,C,D$ or $E$.
B and I are honest.

Suppose $C$ liar. We have a triangle between $A-B-E$, which means that they were together at some point. We also have the triangle $I-E-B$, but we don't have a tie $A-I$, meaning that there's a moment when $B$ was inside the shop and either $I$ or $A$ had already left it, while the other (of $A$ or $I$) hadn't entered yet. If so, how is it possible that $D$ saw $A$ and $I$ without seeing $B$? Impossible! Therefore, C is truth-teller.

Suppose $E$ liar. We know that $A$ and $I$ are never together. $D$ saw both $A$ and $I$ , $B$ saw both $A$ and $I$ too, so how is it possible that $B$ and $D$ weren't together? Impossible! Therefore, E tells the truth.

Suppose $A$ liar. $B$ and $C$ didn't meet. $E$ has seen both $B$ and $C$, meaning that $E$ was present when one had left and the other had yet to enter. D was intermediate between $B$ and $C$, despite not meeting $B$, because he has seen $A$ (who was seen by $B$). So, how is it possible that $E$ and $D$ never met? Impossible, so $A$ tells the truth.

The liar is $D$. This is a scheme of compatible timings. The time is represented on the horizontal axis. People that share points with the same abscissa were together in the library, of course.

Answer 7

The problem is ill-posed.

The liar must be one of A or D, but there is a consistent scenario where A lies and everyone else tells the truth, as well as a consistent scenario where D lies and everyone else tells the truth.

First scenario:

A enters at 7:00 AM, I enters at 8:00 AM, B enters at 9:00 AM, E enters at 10:00 AM, B leaves at 11:00 AM, C enters at 12:00 PM, E leaves at 1:00 PM, D enters at 2:00 PM, C leaves at 3:00 PM, D leaves at 4:00 PM, I leaves at 5:00 PM, A leaves at 6:00 PM. A is the only liar: the truth is that A saw everybody.

Second scenario:

D enters at 7:00 AM, E enters at 8:00 AM, C enters at 9:00 AM, I enters at 10:00 AM, C leaves at 11:00 AM, B enters at 12:00 PM, I leaves at 1:00 PM, A enters at 2:00 PM, B leaves at 3:00 PM, A leaves at 4:00 PM, E leaves at 5:00 PM, D leaves at 6:00 PM. D is the only liar: the truth is that D saw everybody.

Whittling down the suspects:

Say that suspects X and Y are "connected" if one of X or Y claims to have seen the other. Define a 4-cycle to be a four-tuple of suspects (X,Y,Z,W) such that X is connected to Y, Y is connected to Z, Z is connected to W, W is connected to X, X is not connected to Z, and Y is not connected to W. If (X,Y,Z,W) is a 4-cycle, then it is pretty easy to see that at least one of X,Y,Z,W must be lying. Using the 4-cycle (A,B,I,D) we see that one of A,B,I,D is lying, and using the 4-cycle (A,D,C,E) we see that one of A,D,C,E is lying. Thus the liar is either A or D.

There is a hidden symmetry in the problem:

The connection graph described earlier is symmetric under the permutation (AD)(BC)(EI).

Answer 8

I believe the "correct" way to do this is to start by determining which groupings are certain. (I'm certain it's correct, but I don't know if it's how they expected it to be done)

We can quickly identify two pairs of people who definitely saw each other.

• Albert and Bernard both saw each other.

• Charlotte and Isabelle both saw each other.

This means these two pairs must have happened.

Now, we also have that Albert saw Edouard, who saw Bernard. This indicates that Edouard was present with at least one of the two, as Albert and Edouard can't both be lying.

Similarly, Isabelle saw Edouard, who saw Charlotte, so Edouard was present with at least one of the two, as Isabelle and Edouard can't both be lying.

We also have that Isabelle saw Edouard, who saw Bernard, who saw Isabelle. These three must be together, as only one can be lying, which still ties all three into the same group.

Finally, we have Isabelle saw Charlotte, who saw Didier, who saw Isabelle. Again, only one can be lying, so these three were present together.

So we have (ABE), (BCI), (CEI), and (CDI) as certain to be present in their respective groups.

This leaves just one claim unaccounted for. Didier claimed to be present with Albert. This is the only claim not corroborated by anybody else, directly or indirectly, and therefore must be the lie.

To solve this more easily, I drew up the claims as a directed graph, and then looked for loops within the graph. If three people formed a loop, they corroborate each other's claims. The only claim not part of a loop is Didier claiming to have seen Albert.

To be clear, methods based on working out timelines are problematic, as they require assumptions about sequences, whereas the above is purely about requiring that there be only one liar.

Answer 9

This problem is actually underdetermined. Credit goes to Mark N for the idea of everyone entering the room at the same time

---

Counter-example: Everyone enters the room at the same time.

Solution 1: Albert is the liar

Albert can claim that they didn't see Bernard even if Bernard was in fact there. As long as Bernard claims that they saw Albert, this follows the rule that one of them saw the other.

Solution 2: Bernard is the liar (similar argument)

Bernard can similarly claim that they didn't see Albert even if Albert was in fact there. As long as Albert claims that they saw Bernard, this follows the rule that one of them saw the other.

---

Since we have arrived at two valid solutions, this is an underdetermined system.

Answer 10

These are the only absolute statements I've arrived to:

The following are never inside the library at the same time::

A and C
A and I
B and C
B and D
D and E

Answer 11

I feel like the answer may be that...

Bernard is the culprit.

Why?

There exists a little inconsistency between people seen.
Let's draw these reports out:
B -> AI
D -> AI
C -> DI
A -> BE
E -> BC
I -> CE

This leaves us with the following.

Albert, Bernard, Charlotte, and Edouard were all seen twice.
Isabelle was seen three times.
Didier was seen once.

Given this information,

Say Bernard saw Didier instead of Isabelle. We get the following:
B -> AD
D -> AI
C -> DI
A -> BE
E -> BC
I -> CE

This evens everything out, with Didier and Isabelle now being sighted twice each.

Therefore...

It can be concluded that Bernard lied about seeing Isabelle.

Answer 12

-> is saw; <- is seen
A -> B E
B -> A I
C -> D I
D -> A I
E -> B C
I -> C E

A <- B D
B <- A E
C <- E I
D <- C
E <- A I
I <- B C D

The thief lied, so that means the thief claims he saw someone when he didn't. That means the thief saw 1 or 0 people. Conversely, only 1 person at most could have seen the thief. Therefore, since D is the only one seen by 1 person or less, D must be the thief.