6

This puzzle is part of the Puzzling Stack Exchange Advent Calendar 2023. The accepted answer to this question will be awarded a bounty worth 50 reputation.

< Previous Door Next Door >

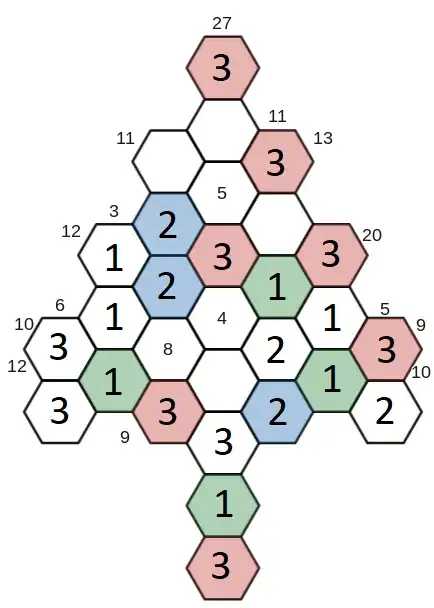
Rules:

Normal Hexologic rules apply

  • You can place one, two or three dots in each blank space.
  • The number value of the cells in a given row must add up to the number that is pointing towards that row.
  • If you put a number in a colored cell, then all cells that are colored the same color also have that number.
  • Numbers that are greater than 3 that are already on the grid are forced numbers that are already part of the puzzle.

Desmos link{1}

Desmos link for partially colorblind puzzlers

enter image description here

For partially colorblind puzzlers (hue is changed from 0.4 to 0.7)

enter image description here

{1}only thing that I found that would let me place proper hexagons tbh

CrSb0001
  • 2,231
  • 4
  • 29
  • 1
    I hate to say it, but there aren't any arrows in the image. – fljx Dec 18 '23 at 18:10
  • @fljx sorry about that, I was for some reason unable to make that work. I've been attempting to fix it on a copy but am unable to for some reason – CrSb0001 Dec 18 '23 at 18:11
  • 1
    It's fairly clear which rows the numbers should be pointing at. But your instructions mention arrows. – fljx Dec 18 '23 at 18:17
  • @fljx yeah, i know, I'll fix the wording quick – CrSb0001 Dec 18 '23 at 18:18
  • 3
    I don't think this is solvable as-is. The down-left 13 requires 8 from 3 unknown cells, which must be 2,3,3 in some order. But the 3 in the second column from the left requires all 1's. – fljx Dec 18 '23 at 18:36
  • @fljx Thanks for that comment, I just realized that I accidentally counted something incorrectly, whoops – CrSb0001 Dec 18 '23 at 18:38
  • The down-right 11 is also problematic... – fljx Dec 18 '23 at 18:39
  • Let us continue this discussion in chat. – CrSb0001 Dec 18 '23 at 18:39
  • 1
    "If you put a number in a colored cell, then all cells that are colored the same color also have that number. Numbers that are greater than 3 that are already on the grid are forced numbers that are already part of the puzzle." That'd imply all already-numbered cells of the same color have the same number. They don't. – msh210 Dec 18 '23 at 19:05
  • @MatthieuM. Oh sorry about that, I was trying to go with a Christmas theme tbh, I could try making the cells brighter (since I know that's possible using Desmos) – CrSb0001 Dec 19 '23 at 12:10
  • @CrSb0001: Ah, Christmas of course. Is it possible to change the borders? Dash/Dotted vs plain to distinguish red from green would work quite well. Otherwise, if possible, a different hue would help indeed, making one lighter and one darker. – Matthieu M. Dec 19 '23 at 12:15

1 Answers1

9

The completed tree:

enter image description here

The solve path:

  • The 6 column on the left must have a 3 in both cells.
  • And the adjacent 3 column must have a 1 in every cell.
  • That makes all the green cells 1.
  • The down-left 20 now needs another 6 from two cells, so both must be 3.
  • And that makes all the red cells 3.
  • And the down-right 10 has one unknown cell that must be a 3.
    enter image description here

  • The 5 column on the right has one unknown cell that must be a 2.
  • The down-left 9 has one unknown cell that must be a 2.
  • That makes all the blue cells 2.
  • And now the up-left 10 has one unknown cell that must be 1.
  • And the down-left 12 has one unknown cell that must be 2. enter image description here

  • The up-right 9 has one unknown cell that must be 3.
  • And now the big 27 column has one unknown cell that must be 2.
  • The 11 column has one unknown cell that must be 3.
  • And finally, the last empty cell must be 1 to complete the down-right 12. enter image description here
    • fljx
    • 15,848
    • 2
    • 54
    • 91