Yes
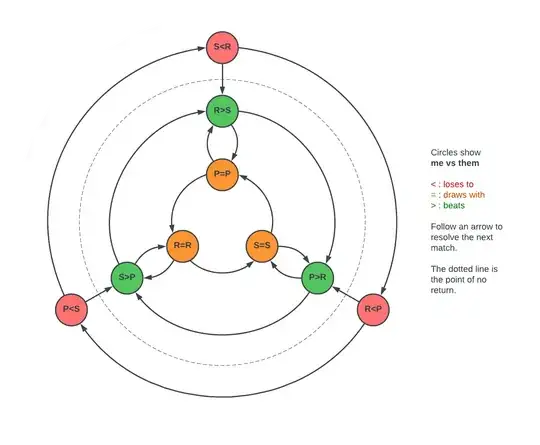
Here is a winning strategy:
First play Paper. Just because.
Then at each move there are 3 possibilities:
If you have just made a draw (wlog, you both played Rock) then you both have the same possibilities for the next move, one beating the other (here Scissors > Paper). Play this one (here Scissors) with an expected score of 3/4.
If you have just lost (wlog, you played Rock against Paper), then one of your two possibilities can make either a draw or a loss (here Scissors, vs Scissors or Rock) and the other can either win or lose (here Paper, vs Scissors or Rock). Play the latter one with an expected score of 1/2.
If you have just won (wlog, you played Paper against Rock), then one of your two possibilities can make either a draw or a win (here Scissors, vs Scissors or Paper) and the other can either win or lose (here Rock, vs Scissors or Paper). Play the former one with an expected score of 3/4.
Your expected win is
a linear combination of 3/4, 1/2 and 3/4 with non-zero probabilities, so it is higher than 1/2.
Your probabilities for round n (n>1) are:
loss: P_L(n) = 2^(1-n) / 3
draw: P_D(n) = (3-2^(1-n)) / 6
win: P_W(n) = (3-2^(1-n)) / 6
Counting 1 for a win, 1/2 for a draw and 0 for a loss, your expected score on round n is:
E(n)= (3-2^(1-n)) / 4
When the number of games tends to infinity, your expected average score
tends to 3/4.