Colouring a rug

Question

I have a rectangular rug in my living room composed of coloured patches (shown below). For convenience I have labelled each distinct colour from 1 to 6. Let's suppose that it was created by starting with a blank rug and colouring one rectangular (can be square) patch at a time. Locations can be recoloured multiple times. An L-shaped piece may be made from two or more patches; it is not necessary to use a single patch, and then overlap it with other colors. What is the least number of colourings required to make this rug?

Computers are allowed.

Text representation (numbers are distinct colors):

12222444111113222
12222444111113222
12222444111113222
12222633333333555
63333111166661555
11113111366661555
11113111366661111
11113111366661111
11113666333333336
11113555222116444
44223555222116444
44223555233336444

P.S. I've been staring at this rug for a while now and I had a feeling that there is a nice puzzle hidden in there, but it took me a while to find it.

Please confirm whether the following $12 \times 17$ grid matches the rug: \begin{matrix} 1&2&2&2&2&4&4&4&1&1&1&1&1&3&2&2&2\ 1&2&2&2&2&4&4&4&1&1&1&1&1&3&2&2&2\ 1&2&2&2&2&4&4&4&1&1&1&1&1&3&2&2&2\ 1&2&2&2&2&6&3&3&3&3&3&3&3&3&5&5&5\ 6&3&3&3&3&1&1&1&1&6&6&6&6&1&5&5&5\ 1&1&1&1&3&1&1&1&3&6&6&6&6&1&5&5&5\ 1&1&1&1&3&1&1&1&3&6&6&6&6&1&1&1&1\ 1&1&1&1&3&1&1&1&3&6&6&6&6&1&1&1&1\ 1&1&1&1&3&6&6&6&3&3&3&3&3&3&3&3&6\ 1&1&1&1&3&5&5&5&2&2&2&1&1&6&4&4&4\ 4&4&2&2&3&5&5&5&2&2&2&1&1&6&4&4&4\ 4&4&2&2&3&5&5&5&2&3&3&3&3&6&4&4&4\ \end{matrix} — RobPratt, Oct 06 '23 at 16:21
I'm not sure I 'get' the puzzle. Some of the patches are not reactangular. Are the patches fixed, or can patches be made any shape? Are six colours required, and not, say four? — Weather Vane, Oct 06 '23 at 17:36
@WeatherVane Think of it like this: You have a supply of rectangular/square pieces of cardboard in all 6 colours and of all possible sizes. You use them to exactly copy the 6-coloured design of this rug by laying them down one by one, where they are allowed to overlap each other. What is the minimum number of pieces you need? — Jaap Scherphuis, Oct 06 '23 at 18:27
@RobPratt that matches, but the last 4 columns seem to be missing? — Dmitry Kamenetsky, Oct 06 '23 at 21:05
ah yes it's all there. Thanks for making that. Feel free to add it to the problem — Dmitry Kamenetsky, Oct 06 '23 at 21:42
@DmitryKamenetsky may we have some clarity on the rules please? Can an L-shaped piece be made of two (or more) patches, or must it be a single rectangle that is L-shaped because another piece overlaps it later? — Weather Vane, Oct 08 '23 at 21:51

loopy walt · Accepted Answer · 2023-10-10T03:25:58.710

14

Here is a 19: UPDATED: Colours now roughly follow OP's.

Patches are numbered A-S in order of appearance. In each panel the latest patch is also highlighted by double density boldface lettering. Except for the last panel which repeats the one before without the highlighting.

This was found "manually" with the computer used only for counting, drawing and checking.

edited Oct 10 '23 at 03:25

answered Oct 09 '23 at 11:52

loopy walt

21,184
33
95

2

Someone beating Rob's solution? Now, that's a first. Usually that means he uses a different assumptions. Let's see what it is for this. – justhalf Oct 09 '23 at 13:43
1

@justhalf Probably the same assumptions. I don’t yet know the minimum. So far, the best lower bound I have from ILP is $12$. – RobPratt Oct 09 '23 at 14:09
3

I verified this solution. +1 – RobPratt Oct 09 '23 at 15:13
Nice! (that white for last move is super confusing though) – Kris Van Bael Oct 09 '23 at 18:29
@KrisVanBael Better now? – loopy walt Oct 10 '23 at 03:26
@loopy wait Excellent. – Kris Van Bael Oct 10 '23 at 05:09
I am giving you the tick for now. Well done! I wasn't able to find a solution with 18 steps (had one error). It would be nice to prove that 18 is not possible or at least some lower bound. – Dmitry Kamenetsky Oct 13 '23 at 11:45

score 10 · Answer 2 · answered Oct 06 '23 at 18:51

10

I was able to get 21 with a pretty naïve approach, but I would bet this is not optimal:

answered Oct 06 '23 at 18:51

0x5453

590
3
7

This is a great solution. Let's see if anyone can do better. – Dmitry Kamenetsky Oct 06 '23 at 23:22
1

I equalled it with two other solutions, but not better. – Weather Vane Oct 08 '23 at 00:51

RobPratt · Answer 3 · 2023-10-10T03:52:07.243

7

Here's a solution in

20 steps,

where $(i_1,j_1)$ and $(i_2,j_2)$ are the top-left and bottom-right corners of the rectangle:

\begin{matrix} \text{step} & i_1 & j_1 & i_2 & j_2 & \text{color} \\ \hline 1 &4 &1 &12 &17 &6 \\ 2 &1 &1 &4 &1 &1 \\ 3 &5 &2 &12 &16 &3 \\ 4 &1 &2 &4 &17 &2 \\ 5 &11 &1 &12 &2 &4 \\ 6 &4 &6 &12 &14 &6 \\ 7 &10 &6 &12 &8 &5 \\ 8 &10 &15 &12 &17 &4 \\ 9 &1 &7 &4 &14 &3 \\ 10 &1 &6 &3 &8 &4 \\ 11 &1 &9 &11 &13 &1 \\ 12 &10 &9 &12 &11 &2 \\ 13 &6 &1 &10 &4 &1 \\ 14 &4 &9 &9 &14 &3 \\ 15 &5 &6 &8 &17 &1 \\ 16 &11 &3 &12 &4 &2 \\ 17 &12 &10 &12 &13 &3 \\ 18 &4 &15 &6 &17 &5 \\ 19 &5 &10 &8 &13 &6 \\ 20 &6 &9 &9 &9 &3 \\ \end{matrix}

With the hints about which color to use at each step, I was able to get the solver to find @loopy walt's solution:

A near miss for $18$, with only cell $(4,6)$ wrong (should be $6$ instead of $3$):

edited Oct 10 '23 at 03:52

answered Oct 08 '23 at 18:10

RobPratt

13,685
1
29
56

1

Nice one! I just found another 20-step solution (by hand). But you beat me to it :-) – Kris Van Bael Oct 08 '23 at 18:36
1

The gif animation is too fast and doesn't repeat, making it difficult to follow. – Daniel Mathias Oct 08 '23 at 18:59
I worked this thru on paper: the L-shaped 3 sections here are not made of a whole rectangle, but of separate pieces, for example step 20 fills in part of an L-shape. Is that permitted? I thought the idea was that where we see a colour, it's a single rectangle (or square) that was covered by another piece. – Weather Vane Oct 08 '23 at 19:05
1

@DanielMathias I replaced the gif with a slower animation. Just refresh to repeat. – RobPratt Oct 08 '23 at 19:22
Much better :o) – Daniel Mathias Oct 08 '23 at 19:23
@KrisVanBael Does your solution satisfy the additional contiguity requirement that Weather Vane mentioned? – RobPratt Oct 08 '23 at 19:27
There is also a deleted 20-step solution which appears to assemble an L-shape in two parts around the colour that apparently makes it an L-shape, but was placed first. – Weather Vane Oct 08 '23 at 19:31
@WeatherVane The deleted solution by fedab fails to count the bottom $3 \times 3$ block of fives, so it is actually 21 steps. – RobPratt Oct 08 '23 at 19:33
2

@RobPratt No it doesn't (see my answer). I don't think that creating a single coloured area in multiple moves contradicts with the original question, and it leaves room for more creative solution – Kris Van Bael Oct 08 '23 at 20:45
Very nice. Can you share your approach? – Dmitry Kamenetsky Oct 09 '23 at 00:06
3

@DmitryKamenetsky if you ask RobPratt about his approach, it will always be "Integer Linear Programming" (lighthearted, I know the complexities are in the details on how to apply ILP, and good work as always, Rob) – justhalf Oct 09 '23 at 13:39
@justhalf You are correct. – RobPratt Oct 09 '23 at 14:07
Nice near miss! I feel that 18 might be possible. – Dmitry Kamenetsky Oct 12 '23 at 12:30

Kris Van Bael · Answer 4 · 2023-10-08T21:33:25.700

The best solution that I found (by hand), requires ...

20 moves

As already discussed in other answers, one trick is to...

... allow building a patches in more than 1 move. It's locally inefficient, but it might unlock other (and bigger) optimisation opportunities. This is especially true for those big brown L-shapes.

My little breakthrough was when I considered this move:

Because it fills four patches and leaves opportunity in the space around it for other optimisations.

So, inserting some extra moves before it, resulted into...

Note that this has already completes 12 patches in just 5 moves!

From there on it's pretty straightforward. So here is the complete solution:

To describe it in a single diagram, I marked all cells with letters to indicate in which order they get their final color.

So, to replay the solution: First fill the bounding rectangle around all A-cells, then the rectangle around all B-cells, etc... (If you see other letters inside such a rectangle, they should be further in the alphabet, and hence will be overwritten in a later move)

The letters go up to T, so that's 20 moves.

Weather Vane · Answer 5 · 2023-10-08T19:23:25.087

I believe that the answer by user @0x5453 can be equalled, but not improved. This is based on an understanding that where we see a L-shaped piece, it is a single piece, i.e. a rectangular piece partly covered by another piece.

There are 25 areas and I have labelled them a to y.

The problem of laying larger pieces is compounded by the fact that some colours overlap each other. For example 1p overlaps 3g, 1r overlaps 3t, and 3t overlaps 1b. Similarly 2s overlaps 3g and 3u overlaps 2e.

First I wrote a C program that attempted to permute the placing of merged combinations of the same colour but it probably won't even find @0x5453's solution before hell freezes over. On closer examination I found that the search space can be reduced, because there are 10 areas that overlap which can't be placed until last, individually, and there is no chance of merging them because they will break already laid areas.

When I removed those 10 areas from the problem, it left a single 4 and a single 5 so they can be done last too. This image show those 12 areas n to y in grey.

Leaving those 12 until last gives 13 pieces to fiddle, with only four colours: 1 (3 of), 2 (3 of), 3 (2 of) and 6 (5 of). Analysing what is left, where in each case —

If we begin with colour 6 as @0x5453 did, any attempt to pair or triple up the other colours will overlay one or more of the 6 pieces, cancelling any saving.

Next, if we begin by filling with 2, and then covering only 3 of 6, these 2 placings cover 6 areas:

with 7 pieces to place individually, then the other 12 (not shown). 2 + 7 + 12 = 21, equalling @0x5453.

Next, if we begin with filling with 1, and then covering just 2 of 2, and then only 2 of 6, these 3 placings cover 7 areas:

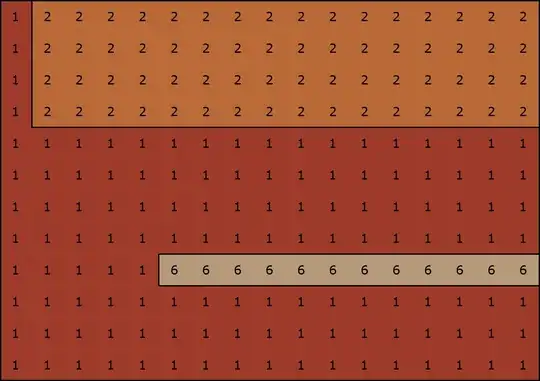
with 6 pieces to place individually, then the other 12 (not shown). 3 + 6 + 12 = 21, equalling @0x5453.

Lastly, if we begin with filling with 3, and then some 3 of 6, the 2 placings cover 5 areas leaving 8 to place individually. 2 + 8 + 12 = 22, worse than @0x5453.

Colouring a rug

5 Answers5