Given a strip of 10 equilateral triangles, how many folds are necessary to reduce it to a single equilateral triangle? You may only fold along the grid lines. Multiple folds along collinear segments are not counted as one fold. Here's an illustration of a 10 triangle strip, for reference:
4 Answers
I know that the answer has already been accepted, but the question doesn't appear to require that the "single equilateral triangle" is the same size as one of the "10 equilateral triangles".
So there is a solution that only requires four folds as follows:
- 35,897
- 5
- 66
- 276
- 13,882
- 1
- 37
- 93
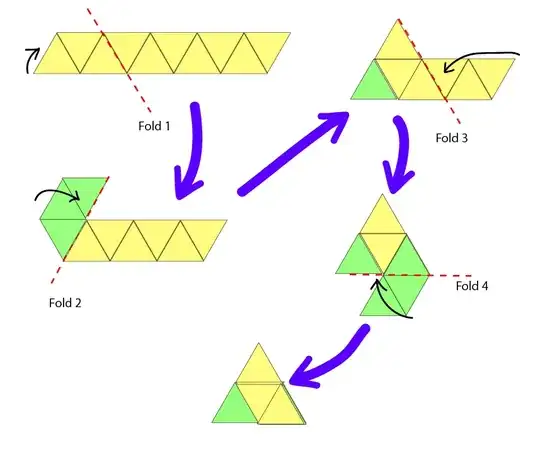
With some "creative reading of the rules", I managed to create a single equilateral triangle folding only
3 times. (Although the co-linear fold counting rule may give this a different score)
Like so:
- 77,343
- 8
- 173
- 360
-
3
-
Clever, but the OP presumably meant "a single equilateral triangle of sidelength 1" – smci Apr 29 '23 at 19:53
Here is a solution that does it in 6 folds using colinear folds. Without, it would be 8.
First, fold along the halfway line
This takes us down to 9 visible triangles. Next we fold along the end trapezoidal shape.
We are down to 7 visible triangles. Folding along the long central edge...
Brings us to 5. Folding either of the inner lines...
Gives us 4 triangles, and easy symmetry makes the last two steps clear.
- 132
- 1
- 5
I believe this is optimal, but I have no proof.
Six folds marked in red, with shadow of previous step in grey.
- 14,926
- 2
- 30
- 62
-
1I'm going to give the answer to the other guy, just cause he answered first and may have been constructing his answer before I made the edit. But thank you for editing my post so quickly and thank you for your contributed answer. I really like the way you showed the fold lines and where the pieces were previously. – PuzzleAndy Apr 26 '23 at 22:07
-
This answer is a real 6-folder even with the collinearity rules. Nice one! – justhalf Apr 29 '23 at 10:27








ceiling(log_2(N)). Because each folding at best halves the number of triangles. – smci Apr 29 '23 at 19:54