I honestly don't know how to start... so I'm just looking for how to start, ie is there a number that we know where it has to go and why?
In addition to standard Sudoku rules, numbers on either side of bars must be consecutive AND numbers without bars between can't be consecutive.
From book: Consecutive Sudoku - 200 Hard to Master Puzzles 6x6
You can start by asking
Where is the 5 in column 6.
The six in box 6 has four possibilities, all next to a bar, so there must be a 5 adjacent to that six, away from the rightmost column. The given 6 rules out the the rest of the options in the column, so
there must be a 5 on row 4 in column 6.
From there, you get the bottom two digits of column 6 easily, seeing as how box 6 must have two pairs of consecutive digits, and therefore r6c6 has only one non-consecutive option:
Out of the remaining 2 and 3 in the column, only the 3 can go between the 5 and 6, which breaks the whole puzzle wide open, for example by solving the 2 and 3 in box 6.
Here's the final solution:
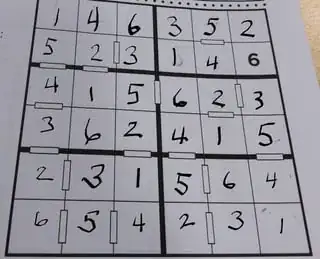
This kind of sudoku is usually called Kropki (Polish for "polka dots", the bars are usually drawn as circles), and the usual solution methods involve inspecting long chains of connectors (column 1 turned out to be a red herring in this puzzle), and also squares and digits adjacent to the givens.
Look at the bottom-right block to get started:
There is already a 6 in the rightmost column, so it must be in one of the other four cells, along with a neighboring 5. This means that the 5 in the rightmost column, which is not adjacent to the 6, must be in row four, with an adjacent 4 in row five.
Then look at the middle-right block:
There is a group of three consecutive numbers. They cannot be 2-3-4 as this would have the 4 next to the 5 in cells that are not consecutive. This group must therefore be 1-2-3, with the 2 in row four, column five.
Back to the bottom right:
The 2 must be in row six, column four to avoid having the 3 next to the 4.
The completed block is then
5-6 4
2-3 1
With that, you can complete columns five and six, complete the top-right block, then proceed with the left half of the grid.
For simplicity, I'll assign each number from 1-6 a color.
A dot in a field indicates that the given number can't appear in that field (I made the dots smaller if we already know them from previous steps). For example, these are all trivial given the starting 6:
We can also deduce other impossible numbers: There can't be a 5 in any of the squares next to the given 6. There can't be a 1 or 6 in R3C1, R3C5, R4C1 and R6C2, as those need two consecutive neighbors. There also can't be a 3 or 4 in R1C1 and R6C1, as the middle four cells of the first column couldn't all be consecutive otherwise.
Next, let's just try to put the 6 in the third row. It can only go in three places, either in the second column or in the third or fourth one, which would also place the 5. A quick check reveals that the second column doesn't work - it would immediately force a bunch of numbers, and there would be no way to place the five in sixth row.
Therefore, 5 and 6 must be in the third and fourth column. As this excludes R3C5 from being a 5 as well, R4C5 can't be a six either, as those cells need to be consecutive. Putting a 6 in R4C4 also doesn't work anymore.
The only cell left for the 6 in the center left area is therefore R3C4, which also places the 5 in R3C3:
Now you should be able to proceed.
Edit: Had to update the last image
I did it by starting with the chain of blocks going from Row 2 Column 1 to Row 5 column 2. There is a very limited number of sequences that will fit that chain. Combined with the existing 6 and the chain going from Row 6 Column 1 to Row 6 Column 3, you can fairly quickly eliminate all but one sequnce.
