Packing pentominoes in a circle

Question

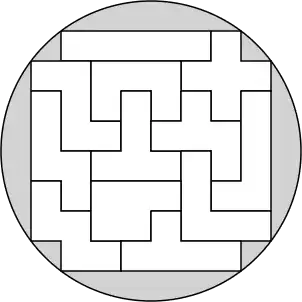
You want to prepare a pizza of 12 flavors. You have 12 oddly-shaped pieces of cheese that you decide to use for the pizza. The shapes happen to be ...

Oh, well, forget it! This isn't going to be even remotely realistic. So here is the problem:

I was playing with pentominoes and figured you can pack them nicely in a circle of radius 5.

This immediately cries for the question: Is this optimal? If not, what is the radius of the smallest circle that can accommodate all 12 pentominoes inside without overlap? Show an arrangement that minimizes the radius.

Spoiler alert: the picture above is not optimal.

Scoreboard:
4.84323 loopy wait
4.86594 Florian F
4.88966 Ravi Fernando
4.92443 Daniel Mathias
4.94975 cap
4.98189 Franciszek Remin

The trivial lower bound is $\sqrt{60/\pi} \sim 4.37$ which is a disk with the same area as the 12 pentominoes but of course you can't reach that because there will always be some waste at the edges. — quarague, Aug 29 '22 at 06:25
My junior's name is Franciszek Remin - if you were so kind to put my son's name on the list of fame. — Przemyslaw Remin, Jan 03 '23 at 12:30

loopy walt · Accepted Answer · 2022-09-22T09:47:47.823

19

UPDATE 2

A minor improvement. New best radius

4.84323

Arrangement

/UPDATE 2

UPDATE

New best radius:

4.8487

using arrangement

/UPDATE

I get a radius of about

4.866

using the following scheme

which is obviously heavily indebted to Ravi Fernando's. The improvement is in the left half.

edited Sep 22 '22 at 09:47

answered Sep 17 '22 at 13:38

loopy walt

21,184
33
95

2

Congratulations! This matches my result. At last! And your arrangement is even more elegant than mine. – Florian F Sep 17 '22 at 19:05
2

@FlorianF Just managed to shrink it a bit more. – loopy walt Sep 18 '22 at 05:06
1

Fantastic! Checked and validated. Unfortunately, I cannot accept or upvote a second time. But I updated the scoreboard. – Florian F Sep 19 '22 at 19:26

Ravi Fernando · Answer 2 · 2022-09-15T06:08:27.253

I can get a radius of:

$\sqrt{\frac{149487}{2} - 975 \sqrt{5873}} \approx 4.88739$.

Method: start with

the following modification of cap's answer (thanks also to Jaap Scherphuis's comment):

and then

shift the rightmost three pentominoes up by $c = \frac{77 - \sqrt{5873}}{2} \approx 0.18225$ units.

The resulting figure has circumcenter located $\frac{7c-c^2}{14} = \frac{5\sqrt{5873} - 383}{2} \approx 0.08875$ units left of the center of the middle square; it intersects the circumcircle at the northwest, southwest, and southeast corners, as well as the corner at top of the eastern edge.

EDIT: I found a second solution with the slightly worse radius

$\sqrt{12110 - 480 \sqrt{634}} \approx 4.88966$.

Method: start with

the following configuration inspired by Daniel Mathias's answer, with four half-square-unit holes:

and then

shift the four rightmost pentominoes up by $c = \sqrt{634} - 25 \approx 0.17936$ units.

The resulting figure has circumcenter $\frac{4c - c^2}{18} = \frac{6 \sqrt{634} - 151}{2} \approx 0.03807$ units left of the center of the middle square; it touches its circumcircle at the top and bottom of the left edge, the bottom of the right edge, and the top corner of the X-pentomino. Note that the four pentominoes in the middle don't touch the circumcircle, so they have a little room to wiggle up and down.

I found both of these with the help of

https://cemulate.github.io/polyomino-solver/ to place the pentominoes, and WolframAlpha for coordinate calculations.

While I congratulate all of you for your efforts, I am a bit embarrassed to announce that this still does not match the best solution I know. But you start to be really close. — Florian F, Aug 28 '22 at 22:25
That's great! Really fun problem, I'm looking forward to seeing what further twists it's hiding. — Ravi Fernando, Aug 28 '22 at 23:07
FYI I found another good arrangement, which is unfortunately very slightly worse than my first. I've added it to my answer in case anyone else can gain some insight from it. — Ravi Fernando, Sep 15 '22 at 06:18

caPNCApn · Answer 3 · 2022-08-27T22:57:57.243

10

The radius of the smallest pizza that can accommodate all 12 cheeses is

$\sqrt{3.5^2 + 3.5^2} \approx 4.95$

The cheeses can be arranged like this:

(There is square unit of tomato sauce with no cheese on the right)

edited Aug 27 '22 at 22:57

answered Aug 27 '22 at 22:43

caPNCApn

19,113
1
63
96

2

Very nice solution. By the way, the cheese van be placed to put that square of tomato sauce anywhere you like. – Jaap Scherphuis Aug 27 '22 at 23:06
Nice try ...... – Florian F Aug 28 '22 at 00:07
I am new to this puzzle, on what software can I play this, ie arranging and rearranging the pentominoes?? – Kutsit Aug 28 '22 at 06:16
3

@Kutsit I don't know of any software. I made the pentominoes out of legos and used them to find my arrangement. Then I used a spreadsheet to create the graphic. – caPNCApn Aug 28 '22 at 07:26
@Kutsit I used an on line solver to find the initial pattern and wrote a java program to render it with the circle background – Florian F Aug 28 '22 at 07:49

Daniel Mathias · Answer 4 · 2022-08-28T14:38:28.223

8

The smallest radius is (apparently less than)

$\frac12\sqrt{9^2+4^2}=\frac12\sqrt{97}\approx4.9244$

One such arrangement is shown here:

edited Aug 28 '22 at 14:38

answered Aug 28 '22 at 05:24

Daniel Mathias

14,926
2
30
62

5

You claim it's smallest but don't support that claim. – msh210 Aug 28 '22 at 05:36
4

On the one side, it is probably difficult to prove optimality, I don't require it. On the other side, I know this one isn't. I know of a better solution. – Florian F Aug 28 '22 at 07:55
4

Via integer linear programming, I have found that Daniel's radius matches half of the minimum diameter of a set of 60 nonoverlapping unit squares with integer coordinates. If @FlorianF and I are both right, that means every optimal solution will have at least one pentomino with non-integer coordinates. – RobPratt Aug 28 '22 at 15:34
1

Glad to see you looking in the right direction. Who said cheese has to be placed at integer coordinates on a pizza? – Florian F Aug 28 '22 at 15:44
1

Using half-integers instead (just as a better approximation) yields a lower bound of $\sqrt{90}/2 \approx 4.7434$. – RobPratt Aug 29 '22 at 00:26
4

@RobPratt If you can translate that to an actual solution with pentominoes then you clearly beat me. – Florian F Aug 29 '22 at 04:47
@RobPratt It possibly doesn't matter, but if we exclude a full square we get $\sqrt{90} = 3\sqrt{10}$ :) – CiaPan Aug 31 '22 at 13:27
@CiaPan Yes, with $59$ squares and integer coordinates, the minimum diameter is $\sqrt{9^2+3^2}$. With $59$ squares and half-integer coordinates, the minimum diameter is $\sqrt{9^2+2.5^2}$. – RobPratt Aug 31 '22 at 17:28
@RobPratt (off-topic) You were mentioned in a recent Numberphile video – Daniel Mathias Sep 22 '22 at 20:53
@DanielMathias Thanks for letting me know. I had not yet seen it. – RobPratt Sep 22 '22 at 22:14

score 8 · Answer 5 · answered Aug 31 '22 at 10:28

8

I presented your challenge to my 9-year-old son. I gave him a circle with a radius of 5. To my astonishment, he finally came up with a solution. Sorry I have not bothered to calculate the radius of the smallest circle in which these beasts can be packed. The radius is definitely less than 5. So naturally, this solution is in the game.

answered Aug 31 '22 at 10:28

Przemyslaw Remin

597
3
9

4

Nice! Now let's see. The distance between the left of the lower edge and the right of the upper edge is $\sqrt{9^2+4^2} = 9.8488$, giving a radius of at least 4.9244. But that line isn't centered. For the actual radius I get 4.9547. – Florian F Aug 31 '22 at 11:42
1

How did you inscribe the pentominoes in the smallest circle? Where exactly is the center of the circle? What three vertices of the pentomino pattern land on the rim of the circle? My guess is head of the snake, tail of the fish, and jaw of the crocodile. – Przemyslaw Remin Aug 31 '22 at 20:50
Hm... I placed the center 2/9 units up from the center of the middle square, which is the feet of the giraffe. The bounding vertices were the top edge and the left of the bottom edge. But I missed the crocodile snout, which reaches out of that circle. Now, with the critical corners: snake head, whale tail, croco head, I place the center at (0.06557377, 0.229508197) from the center of the giraffe feet and the radius is 4.981894119. – Florian F Aug 31 '22 at 21:34
Congratulations to your son! – Will Octagon Gibson Sep 01 '22 at 03:44

score 8 · Answer 6 · answered Sep 17 '22 at 19:15

8

For reference, here is my solution.

With a radius of 4.86594

answered Sep 17 '22 at 19:15

Florian F

29,623
4
63
138

Packing pentominoes in a circle

6 Answers6