25

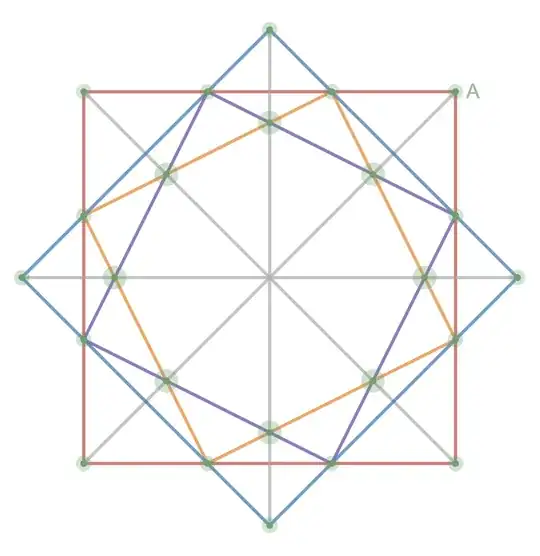
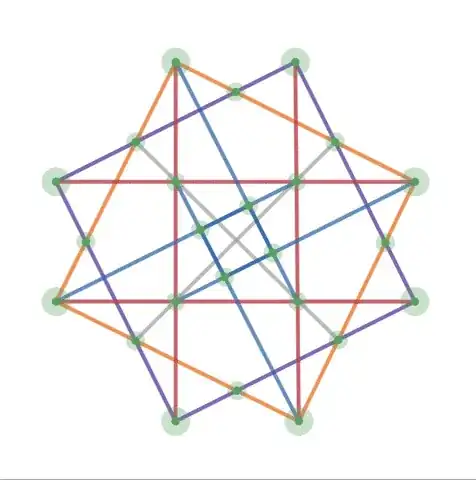
A very old puzzle, #146 from American Agriculturist, April 1865:

How may twenty-four trees be planted in exactly eighteen rows, with four trees in each row? A row consists of a number of trees in a straight line. The same tree can be part of multiple rows. The rows can intersect at any angle. Rows can’t contain more than 4 trees.

Will Octagon Gibson
  • 9,220
  • 1
  • 19
  • 98

3 Answers3

23

I can only do 20 rows. Is that OK?

enter image description here

Now if you want eeeeexactly 18 rows, you can do this.

enter image description here

And if you are crazy about rows of 4, here is how to do. Can you count them all?

enter image description here

Florian F
  • 29,623
  • 4
  • 63
  • 138
  • 2
    This is a nice planting arrangement but the goal is to have exactly 18 rows, not more and not less. – Will Octagon Gibson May 31 '22 at 18:48
  • 1
    Wow! Your second solution is even prettier than the solution given in the American Agriculturist. – Will Octagon Gibson May 31 '22 at 21:11
  • 1
    In your third diagram, I see 24 trees planted at the vertices of three concentric octagons. Using graph theory, each row of trees is drawn with three edges. The degrees of the vertices of the outer octagon is 5, middle octagon 6, and inner octagon 10. The sum of all the degrees is 8*(5+6+10)=168. The number of edges is 168/2=84. Lastly, the number of rows of trees is 84/3=28. Thanks for the cool counting problem. – Will Octagon Gibson Jun 03 '22 at 00:25
  • That is correct, assuming I drew all lines and didn't miss any. – Florian F Jun 03 '22 at 10:24
16

I think this works:

Start with a construction that actually has too many rows (in this case, 20):

1

And then move one of the trees so that it breaks 2 of the rows but preserves the rest. In this case, I moved point A a little further out so it was no longer in line with the two sides of the red square:

2

Edited to add:

There is this, which is perhaps a bit prettier:

3

Or this pinwheel I made:

4

SQLnoob
  • 8,516
  • 29
  • 46
  • Your answer is prettier than the solution that I made a long time ago but there is a solution that is even more symmetrical than yours; this other solution has rotational symmetry in addition to lines of reflection. Can you find such a solution? – Will Octagon Gibson May 31 '22 at 18:43
  • @WillOctagonGibson I updated my answer to include another variation that has some rotational symmetry as well. – SQLnoob May 31 '22 at 20:12
  • I like your second solution. Both your solutions were based on squares; try hexagons. By the way, what software do you use to make your diagrams? – Will Octagon Gibson May 31 '22 at 20:16
  • @WillOctagonGibson I'm using desmos.com to do the geometric constructions. – SQLnoob Jun 01 '22 at 00:00
4

I found a solution that works (mostly through guessing and using symmetry)

       X   X   X   X 
     X   X   X    X
       X       X
 X   X          XX
       X       X
  X  X   X   X    
       X   X   X   X
Prim3numbah
  • 33,595
  • 4
  • 19
  • 171