Weeds have taken over the roads. If mowed, they don't grow back, but unmowed weeds spread at speed 1 along the road. What's the minimum speed of the mower to get rid of all weeds? Roads are connected at each intersection and the mower must move on roads.
To solve this puzzle you have to use the concept of supertask.
Closely related to this puzzle, easier but still very challenging!
Better solution:
It can be done when the mower is:
faster than 5.7749 (see update below)
A slower speed than this is definitely still possible.
We'll say the left intersection has $LU$ and $LD$ of grass heading up and down respectively, and the right intersection has $RU$ and $RD$. Suppose the mower goes as speed $m$.
Here's the strategy:
Step 1: Start at the left intersection and go clockwise around the whole thing. Then the middle section has grass, and $LU,LD,RU,RD=6/m,0,3/m,3/m$.
Then we have a general thing that we'll do once in a while at an intersection.
Step 2:
Clear $LU=6/m$ and $LD=0$ with a geometric series so that you're ready to head across the grassy middle. This takes $T=2l/(m-3)$ (see calc below). In this case $l=LU=6/m$, so $T=12/(m(m-3))$.
Step 3:
Head across the middle bar (so it's grass-free). It takes $1/m$. So now $RU=RD=T+4/m = 4/(m-3)$.
Step 4:
Clear RU and the middle bar. We can use the same formula from Step 2, but with $l=RU=T+4/m=4/(m-3)$. This adds $T_2 = 2l/(m-3)=8/(m-3)^2$.
Step 5:
Clear RD. It catches the growing grass by the time $RD$ has grown to $(T+4/m)\cdot\frac{m}{m-1}$.
Calc:
If $RD<=3$ by the end of all of this, then we can mow everything.
This would mean that $4m/(m-3)^2=4$ which is a mower speed of 5.7749.
More derivations of the equations if you're interested:
Clearing a loose end of length $l$ as in step 2, for speed $m$.
Suppose it takes time $t_1$ to clear $LU$ and return to the original point. Then the grass will have grown to a maximum of $l+t_1/2$. The mower will have traveled $mt_1/2$. So setting these equal gives $t_1=2l/(m-1)$. They meet at $l\cdot\frac{m}{m-1}$.
Meanwhile, the grass will have grown down $LD$ a distance of $t_1$. Clearing this will take $t_2 = 2t_1/(m-1) = r^2l$, where $r=2/(m-1)$.
Etc.
The time to clear the whole mess (as in step 2) is then:
$T = \sum_{i=1}^{\infty}t_i = l\sum_{i=1}^{\infty}r^i = lr/(1-r) = 2l/(m-3)$.
For step 2, $l=6/m$, so $T = 12/(m(m-3))$.
At step 4, $l = 4/m+T = 4/(m-3)$. So $T_2 = 8/(m-3)^2$.
So $RD$ is $4/m+T+T_2 = 4/m+12/(m(m-3))+8/(m-3)^2=4(m-1)/(m-3)^2$
We catch this by the time it's traveled $m/(m-1)$, which means the grass has grown to $4m/(m-3)^2$.
Setting this equal to $3$ gives $m\approx5.7749$ (see here).
It's certainly possible to allow the grass to grow somewhat further than this.
Here's a strategy with speed
5
The red dot is the mower's current position.
Update
If my calculation is correct, speed
4.6428
is also feasible. The plan is a bit too convoluted to be drawn neatly into schematic pictures. But I beilive it's still suboptimal. Maybe someone with a better scheme can improve the bound still further!
My final answer
$v_o = \sqrt{5} + 2$
With proof of optimality
(I deleted my old answers)
Edit: The error in my proof should be fixed, I still claim the same speed.
I have a solution for when the speed is strictly greater than:
$v_o = \sqrt{5} + 2 = 4.236$
This may be optimal, I have an idea on how to prove optimality, but I will need some time to pull things together...
Step 1:
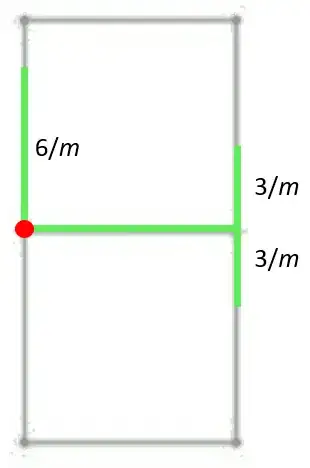
Let's denote $L$ and $R$ the left and right intersection, and $U$, $M$ and $B$ the upper, lower and bottom paths. At any point, let $l_u$ be the length of the grass path starting at $L$ on the upper path. We define similarly $l_m, l_b, r_u, r_m, r_b$. We will describe a position by the vector $(l_u, l_m, l_b, r_u, r_m, r_b)$ (we will never consider a case where some grass is not connected to $L$ or $R$). Let $v>v_o$ be our speed.
At the start, the position is described by $(3, 1, 3, 3, 1, 3)$ We start at $R$. We follow the path $UB$ and arrive at $L$. The position is now described by the vector $(1.416, 1, 0, 0.708, 1, 0.708)$ (base position)
($\frac{6}{v} = 1.416, \frac{3}{v} = 0.708$).
We zigzag on the paths $U$ and $B$ to clear the path $l_u$. It takes $zig(l_u) = \frac{2l_u}{v-3} = 2.292$ time (See Dr Xorile answer for the formula)
We move on $M$ for a distance of $a = \frac{(3-r_b)x-\frac{2l_ux}{x-3}}{1+x} = 0.244$ and get back to $L$, then follow the path $UB$ and arrive back at $L$.
The new value of $l_u$ is given by:
$l_u = \max(1-a+\frac{6+a}{v}-1, r_b + zig(l_u)+\frac{6+2a}{v}) = \max(1.23, 1.23) = 1.23, \frac{3}{v}$ where $r_b=0.708$ is the value of $r_b$ at the base position.
The new values of $r_u$, $r_m$, and $r_b$ are the same as before. We see that the grass coming in $L$ from $M$ and $B$ is the same, this is due to the choice of $a$.
The position is now described by $(1.416-\epsilon, 1, 0, 0.708, 1, 0.708)$, where $\epsilon > 0$ is a value due to the fact that $v > v_o$. (if $v=v_o$, we would get $\epsilon=0$ and make no progress). Now that $l_u$ is decreased, we can do the same thing. Because $l_u$ is smaller, $zig(l_u)$ will be smaller, and the the new value of $l_u$ will be even smaller. By iterating, $l_u$ will decrease steadily (we can verify that there is no fixed point) until $a$ become greater than one. At this point, we can no longer move on $M$ for a length $a$. We repeat the same sequence a last time but with $a=1$. The last value of $l_u$ is dominated by the grass coming from $M$, and its value is $\frac{7}{v}-1 < 0.652$. We move to step 2.
Step 2:
We want use a value of $a$ greater than $1$, but walking from $L$ on $M$, after one unit of time, we arrive at $R$. We still have a bit of margin to push the grass further on the path $U$ and $B$ leaving $R$, that we can clear using a zigzag.
Interestingly, the equations ruling this zigzag are the same that the one for clearing a path of grass, this can be seen by taking this zigzag in reverse: Where we pass, we add grass, but the grass is shrinking instead of expanding. By exchanging the role of grass and non-grass, the problem is similar.
For recall, clearing a path of length $l$ takes $\frac{2l}{v-3}$. It can easily be shown that clearing two paths of length $l$ and $m$ takes $\frac{2(l+m)}{v-3}$. Here, we want to mow the same amount of grass on both sides of $R$ (when we are at $R$). Let $s$ be that amount. The time will be $\frac{4s}{v-3}$.
The path we follow now is : We do the zigzag at $L$, follow $M$, do the zigzag at $R$, follow $MUB$, and arrive back at $L$. We want to get back the same value for $l_u$.
Plugin $s$ into the equations, we get that we need $s = \frac{3 + 2x^2 - 7x - 2l_ux}{x(x + 1)}$, and we will converge to $l_u = 0.382$.
Step 3:
We do the zigzag at $L$, follow $M$, do the zigzag at $R$ follow $MUM$, and arrive back at $L$. This path is $\frac{2}{v}$ shorter than ending the path of Step 2. $l_u-\frac{2}{v}= -0.09$, so we will arrive before the grass reaches $L$!. At this point, it is relatively easy the clear the remaining grass...
