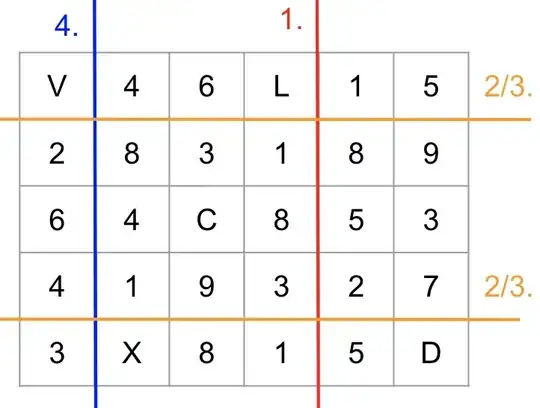
Shown below is 6x5 grid drawn on a paper with various numbers (1 to 9) and letters filling the 30 boxes.
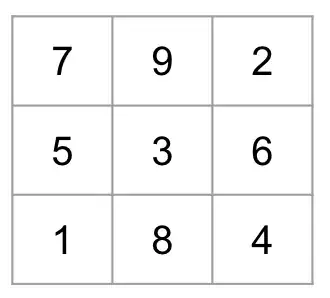
By folding the paper grid 5 times or less can you get to a 3x3 grid showing only the numbers 1 to 9. The folded paper should look like
with the numbers 1 to 9 that you can read directly. All numbers must show up on the 3x3 grid with 1 number per box. Order not necessary. The answer with the least number of foldings will be accepted. Folding only.
Some creative thinking may be needed.
I believe I have a solution that uses
4
folds.
The key to this puzzle is to realize that:
many of the digits can be inverted and still be valid. This is true for 1, 2, 5, and 8, while 6 and 9 will be valid but swap values. Additionally, while most of the letters cannot appear in the final grid, the L is special, as it looks just like a seven when flipped. Thus, we can use it in place of the seven, which would otherwise have forced us to use the only 7 in the grid. This allows us to create solutions where some of the cells are "upside-down", but will still appear as a valid digit.
Folds:
Where all folds are away from the viewer.
Result:
If we look at the resulting paper, we end up with:
Which clearly isn't the solution.
However, if we flip the paper around, we end up with:
Which looks a lot more like our desired result.
