You are given an empty 4x4 grid. You can place some diagonal mirrors into the cells of the grid. You then fire a laser from some location outside of the grid. The laser travels in a straight line. When it hits a mirror it bounces off at a right angle and spins the mirror by 90 degrees. The same mirror can be hit and spun multiple times.
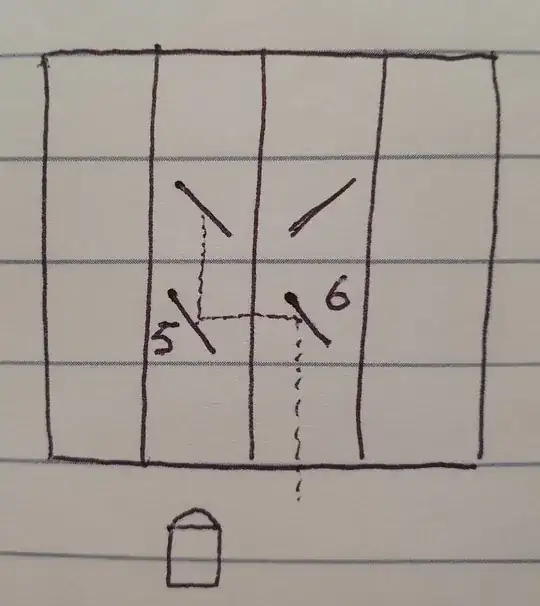
Consider the following example. We place 4 mirrors in the centre of the grid and fire the laser below the second column. It hits the mirrors like so:
The mirrors spin around and the laser continues hitting another 2 mirrors before exiting the grid. In total it had 6 mirror hits:
What is the most number of mirror hits you can obtain on a 4x4 grid?