-3

The answer to the following "decanting" puzzle

Split 10L in half using 4L and 6L jugs

was

It is impossible to pour out 5 liters from 10 liter jug using 6 and 4 liter jugs

Maybe not if you are given more information!

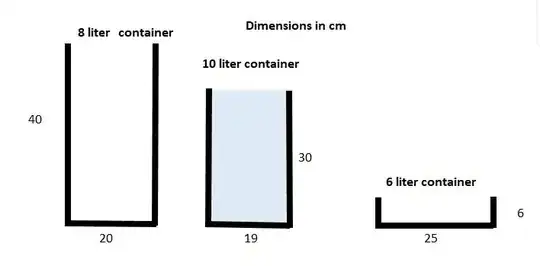
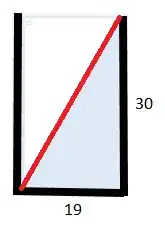
You have three rectangle prism containers: 10, 8 and 6 liters. Their cross-section is shown in the image below. All dimensions are in cm.

enter image description here

The 10 liter container is full of water (10 liters) others are empty.

Can you pour out 5 (+- 0.1) liters of water from it into any other container? Result should be 5 liters of water remaining in the 10 liter container and 5 liters in another container.

You have no marking or measuring tools.You can assume that any pouring you do will be done carefully with little spillage.

Please explain your method.

smci
  • 890
  • 5
  • 14
DrD
  • 39,225
  • 7
  • 76
  • 323

5 Answers5

10

I'm not sure if this is fine, but

You can just tilt and pour slowly the 10 liter container, until the water surface line connects the two diagonal points.

enter image description here

athin
  • 34,177
  • 4
  • 70
  • 221
  • how do you exactly know that? Especially the bottom point? I think you are on the right track but need a convincing geometry explanation. – DrD Nov 04 '21 at 13:17
  • I didn't have a tool to draw a 3D, but the bottom point is trivial (?) to locate because rot13(gurl ner erpgnatyr cevfz naq lbh whfg arrq gb znxr fher gur yvar vf va cnenyyry jvgu gur jubyr rqtr.) – athin Nov 04 '21 at 13:20
  • I still do not get it. You are pouring the water by tilting the container right? How do you know when you reached the right point? – DrD Nov 04 '21 at 13:29
  • 12
    @Drd When the water's surface is fully aligned with the edge of the container which is up, and on the opposite side of the one that water exits. – George Menoutis Nov 04 '21 at 13:42
4

Inspired by athin's answer and DrD's response to it.

The 10 L container will spill half its contents when its edge is lowered to $$\frac{30 * 19}{\sqrt{30^2 + 19^2}} \approx 16 cm$$ spill

This can be achieved like so:

The 8 L container's third dimension is 10 cm. Lay it on its side so it acts as a 10 cm platform. Put the 6 cm tall 6 L container on top of it. Its top edge is now 16 cm above the table. Lean the 10 L into the 6 L container so their edges meet and 5 L will flow from the 10 L container into the 6 L container.

caPNCApn
  • 19,113
  • 1
  • 63
  • 96
  • 1
    Assuming infinitely thin container walls, this would split as 4.9775 + 5.0224 , in case there is competition for a better answer. – alecail Nov 04 '21 at 20:21
2

It can be done quite nicely like this:

Use the 6L container standing on its side to measure 25/40 = 5/8 of the way up the 8L container. Then pour up to that point, which is 5L, and we're done!

Benjamin Wang
  • 1,237
  • 7
  • 13
  • Hello @Benjamin Wang. While theortically your answer makes sense, you are essentially "eyeballing" the mark. This may not be the most accurate way. Remember no marking allowed. – DrD Nov 04 '21 at 13:31
  • 4
    @DrD Can you give an example of a pouring operation that doesn't involve using your eyes to visually confirm that a water level aligns with some other marker? Note that Benjamin's method doesn't require "marking" anything (e.g. with a pen): you just set the container on its side. If this answer is unacceptable, then the question itself seems poorly posed. – Max Nov 05 '21 at 06:51
0

As all the reasonable solutions seem to be disallowed:

It is trivial to get to 4.8l, simply put 8l container inside the 6l one and fill the 6l one to the edge so it holds 4.8l.

There is no other stacking of containers that is better:

  • 10L inside 6L vertically = 4L
  • 10L inside 6L horizontally 1 = 2.6L
  • 10L inside 6L horizontally 2 = 2.8L
  • 8L inside 6L vertically = 4.8L (the best solution)
  • 8L inside 6L horizontally 1 = 1.2L
  • 8L inside 6L horizontally 2 = 3.6L
  • 8L and 10L vertically inside 6L = 2.8L
  • 8L vertically and 10L horizontally inside 6L 1 = 1.4L
  • 8L vertically and 10L horizontally inside 6L 2 = 1.6L
  • 8L inside 10L (if it fits, I haven't calculated): 4L
  • 6L on the side inside 10L one (side that fits): 5.5L
  • 6L on the side inside 10L one (side that doesn't fit, taking just surface areas): 2.8L
  • 6L on the side inside 8L one (doesn't fit, taking surface areas): 2L

Yes, you can think of a sequence of moves that gets you to arbitrary point... if you have 2 extra empty unlimited drums. Otherwise you can't.

Zizy Archer
  • 2,150
  • 7
  • 15
  • There are a few other, better stackings. – alecail Nov 05 '21 at 10:53
  • @alecail I have now added I believe all possibilities, but they aren't better unless I miscalculated. Which option do you see? I assume that that the container put in is vertical - if you are allowed to put things at a particular angle you might be able to do better - but these solutions didn't seem allowed. – Zizy Archer Nov 05 '21 at 12:49
  • I haven't checked your calculations, but if they are correct, couldn't you do the "8L vert and 10L horiz inside 6L 1 = 1.4L" to get 1.4 L into the 6L, remove the others, pour the 1.4L into the 10L container. Then follow up with "8L inside 6L horizontally 2 = 3.6L" to get 3.6L in the 6L container, remove the 8L container and pour into the 10L container -- you should now have 1.4L + 3.6L = 5.0L in the 10L container with no extra drums. – Vaekor Nov 05 '21 at 14:32
  • I was thinking of the cases where the inside container is at an angle somehow, but it's unclear if this is allowed, even though it is not eyeballing, as the reference points are physical points on the container that need to be in contact. – alecail Nov 05 '21 at 15:51
  • @Vaekor Yeah but where are you putting that water in the mean time? As I said, you can reach (nearly?) any point from 0 to 10L with that if you also have 2 unlimited containers. But you can't with just these three. There are some options here that aren't real options anyway - how do you get water in 6L container in the first place if both other containers are squeezed in it? Only if you pour it in first and have it overflow out during squeezing ... but in this case you can't end up with 5+5L then. – Zizy Archer Nov 05 '21 at 21:16
  • I was expecting 5L in one container and the rest wasted, I missed the part where the rest had to be in another container. I concede your point. – Vaekor Nov 06 '21 at 17:49
-1
  • Fill 8 liter container, 2 liters left in the 10 liter container.
  • Fill 6 liter container from 8 liter container, now both 10 and 8 liter containers have 2 liters both.
  • Pour 2 liters from 8 liter container to 10 liter container. Now 10 liter container has 4 liters and 6 liter container is full.
  • Press 8 liter container in to the 6 liter container. This will overflow the 6 liter container and leave 0,9 liters in it. (6 liter container diameters are 25x40x6 and 8 liter container diameters are 20x10x40. When 8 liter container is in 6 liter container, it leaves the volume of 5x30x6 = 0,9 liters)
  • Pour the 0,9 liters left in the 6 liter container to the 10 liter container and it will have 4,9 liters which will be in the allowed limits(5 liters +/- 0,1 liter)

This of course assumes that the walls of the containers (especially the 8 liter container) are infinitely thin.

ViktorMike
  • 1