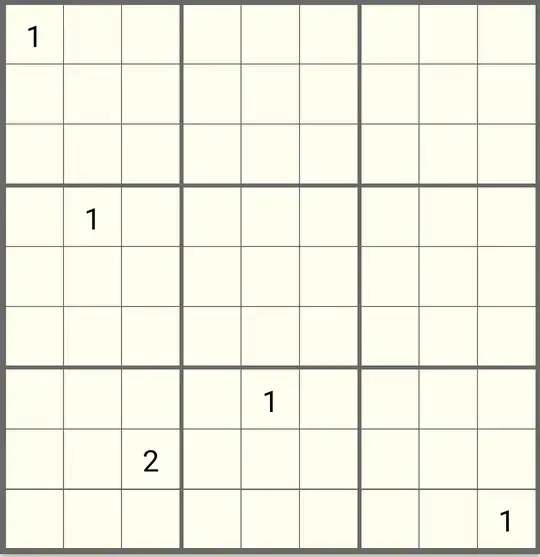
Does every validly posed Sudoku have at least one solution and if not what is the minimum number of givens for it to be unsolvable?

Question

Does every validly posed Sudoku (doesn't break any Sudoku rules so only no duplicate 1 to 9 in rows, columns or square) have at least one solution, and if not, what is the minimum number of givens for it to be unsolvable?

According to Wikipedia:

The puzzle setter provides a partially completed grid, which for a well-posed puzzle has a single solution.

Many others sources including Sudopedia do not state that a Sudoku-like grid with given 1 to 9 numbers has to have one solution to be a Sudoku.

Does have given numbers mean it is solvable, and assuming no, what is the least numbers in a validly posed grid needed to be for it be unsolvable?

"Well-posed" there means "well-designed", not "valid at first glance" — bobble, Sep 22 '21 at 13:38
A "validly posed grid" as in "you must make at least one deduction to know there can be no solution"? — Bass, Sep 22 '21 at 16:25

score 3 · Answer 1 · answered Sep 22 '21 at 13:29

3

5 numbers are certainly enough to make it unsolvable. This is a simple example : grid created with sudoku9x9.com

You can never put one in the bottom left corner. Maybe someone has an optimization?

answered Sep 22 '21 at 13:29

ZenleeK

31
2

Does every validly posed Sudoku have at least one solution and if not what is the minimum number of givens for it to be unsolvable?

1 Answers1