DominoBrane - Chained Domino Fitting

Question

So I've been working on a set of domino puzzles, I call DominoBrane recently, it's sort of similar to Dominosa - except that, unlike Dominosa, the rules of the normal domino game must be followed.

Each domino must connect, as in the normal game, to it's neighbour [0:3][3:3][3:5] etc and make a full circuit of all the 6-dominoes.
At each square, there must be no ambiguity as to which is the connected domino (eg, for a 4 there will be only one adjacent domino with a 4)
The dominoes must be constrained to a 7x8 grid.

Here is an example.

╔═══╦═══════╦═══╦═══╦═══════╗
║ 5 ║ 5   4 ║ 4 ║ 3 ║ 3   1 ║
║   ╠═══════╣   ║   ╠═══════╣
║ 6 ║ 0   2 ║ 2 ║ 3 ║ 1   1 ║
╠═══╬═══════╬═══╩═══╬═══════╣
║ 6 ║ 0   0 ║ 0   3 ║ 1   2 ║
║   ╠═══════╬═══════╬═══╦═══╣
║ 4 ║ 1   6 ║ 6   6 ║ 6 ║ 2 ║
╠═══╬═══╦═══╬═══════╣   ║   ║
║ 4 ║ 1 ║ 4 ║ 4   4 ║ 2 ║ 5 ║
║   ║   ║   ╠═══╦═══╬═══╬═══╣
║ 1 ║ 0 ║ 3 ║ 3 ║ 4 ║ 2 ║ 5 ║
╠═══╬═══╩═══╣   ║   ║   ║   ║
║ 1 ║ 0   6 ║ 6 ║ 0 ║ 2 ║ 3 ║
║   ╠═══════╬═══╩═══╬═══╩═══╣
║ 5 ║ 5   5 ║ 5   0 ║ 2   3 ║
╚═══╩═══════╩═══════╩═══════╝

And here it is again, showing the path of the chain.

╔═══╦═══════╦═══╦═══╦═══════╗
║ 5 - 5   4 - 4 ║ 3 - 3   1 ║
║   ╠═══════╣   ║   ╠═════|═╣
║ 6 ║ 0   2 - 2 ║ 3 ║ 1   1 ║
╠═|═╬═|═════╬═══╩═|═╬═|═════╣
║ 6 ║ 0   0 - 0   3 ║ 1   2 ║
║   ╠═══════╬═══════╬═══╦═|═╣
║ 4 ║ 1   6 - 6   6 - 6 ║ 2 ║
╠═|═╬═|═╦═══╬═══════╣   ║   ║
║ 4 ║ 1 ║ 4 - 4   4 ║ 2 ║ 5 ║
║   ║   ║   ╠═══╦═|═╬═|═╬═|═╣
║ 1 ║ 0 ║ 3 - 3 ║ 4 ║ 2 ║ 5 ║
╠═|═╬═|═╩═══╣   ║   ║   ║   ║
║ 1 ║ 0   6 - 6 ║ 0 ║ 2 ║ 3 ║
║   ╠═══════╬═══╩═|═╬═|═╩═|═╣
║ 5 - 5   5 - 5   0 ║ 2   3 ║
╚═══╩═══════╩═══════╩═══════╝

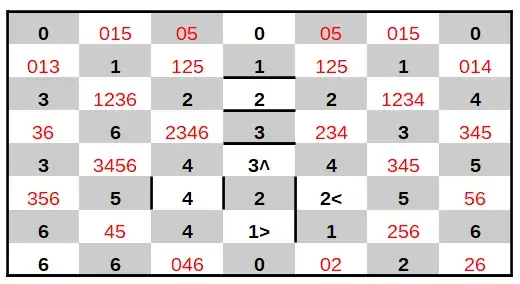
So here's the puzzle: 6-DominoBrane #1, first published here

Following the rules above, find the solution where the numbers match the grid as follows (a blank means 'any number':

╔═══╦═══╦═══╦═══╦═══╦═══╦═══╗
║ 0 ║   ║   ║ 0 ║   ║   ║ 0 ║
╠═══╬═══╬═══╬═══╬═══╬═══╬═══╣
║   ║ 1 ║   ║ 1 ║   ║ 1 ║   ║
╠═══╬═══╬═══╬═══╬═══╬═══╬═══╣
║ 3 ║   ║ 2 ║ 2 ║ 2 ║   ║ 4 ║
╠═══╬═══╬═══╬═══╬═══╬═══╬═══╣
║   ║ 6 ║   ║ 3 ║   ║ 3 ║   ║
╠═══╬═══╬═══╬═══╬═══╬═══╬═══╣
║ 3 ║   ║ 4 ║ 3 ║ 4 ║   ║ 5 ║
╠═══╬═══╬═══╬═══╬═══╬═══╬═══╣
║   ║ 5 ║   ║ 2 ║   ║ 5 ║   ║
╠═══╬═══╬═══╬═══╬═══╬═══╬═══╣
║ 6 ║   ║ 4 ║ 1 ║ 1 ║   ║ 6 ║
╠═══╬═══╬═══╬═══╬═══╬═══╬═══╣
║   ║ 6 ║   ║ 0 ║   ║ 2 ║   ║
╚═══╩═══╩═══╩═══╩═══╩═══╩═══╝

If you solve it, I would really love to know how!
You will be the first person to solve any 6-DominoBrane.

There is exactly one solution to this puzzle.

Be careful to make sure that each square is unambiguous as to where it would go next - the problem is much easier without that constraint.

(Kudos to @bobble for telling me I need to provide single solution puzzles)

I've added [[tag:grid-deduction]] and [[tag:logical-deduction]], but they don't fully fit. The general expectation is that there is only 1 solution, which can be unambiguously deduced using only logic. Multiple solutions is seen by some here as a mark of a poorly constructed puzzle. Finally, your last question - determining a "hardness" level - is opinion-based and as such I've edited it out. — bobble, Mar 17 '21 at 00:30
@bobble, thanks. I'm trying to find a puzzle which guarantees a single solution, while not just becoming a Dominosa puzzle, but that's stumped me! — Konchog, Mar 17 '21 at 00:36
In that case I'd suggest getting more familiar with the unique deductions of this genre. Deusovi has a great guide to creating grid-deductions as well. — bobble, Mar 17 '21 at 00:38
@bobble, thanks for the advice - I have amended the puzzle to provide a unique solution. I was thinking about it the wrong way around! — Konchog, Mar 17 '21 at 01:18