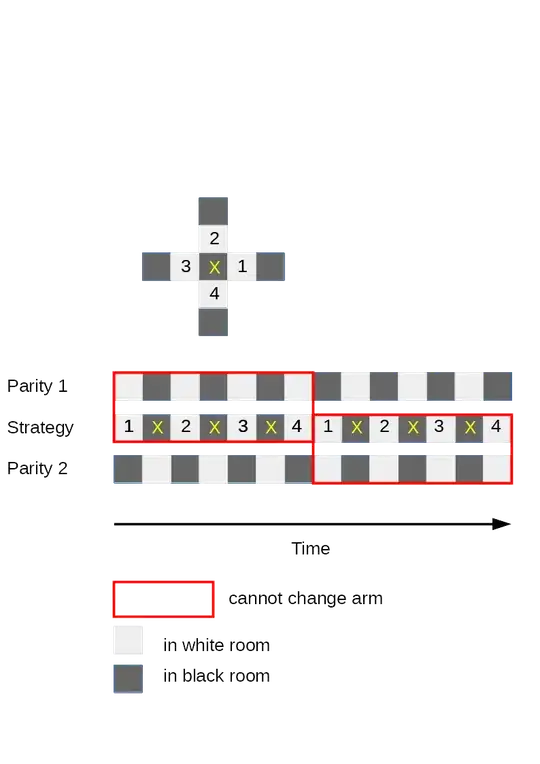
A person was trapped in a building, and you have to save him. You are a police officer and you will arrive at the building at 7 o'clock in the morning. The building looks like this:
Every 2 minutes, you, the person and the interior walls will become invisible. You don't know where the person is but you know that he will move to an adjacent room every 2 minutes. However, you can check any room in the building every 2 minutes because you have a cop car.
Unfortunately, at 7:29 am, the entire building will explode, killing both of you! You have to find a way to save the person, there is not much time left! Note: Your first checking is at 7:02 a.m.