General orchard planting problem for circles

Question

My previous puzzle asked for the maximum number of 4-point circles attainable from a configuration of $n=10$ points drawn on a plane. I am now interested in generalizations of this puzzle to arbitrary $n$.

I wrote a hill-climbing program that searches for configurations with integer coordinates. Here are the best solutions it has found so far:

$n=8$, 12 circles: (2,16) (10,20) (7,26) (12,6) (7,16) (12,11) (22,11) (16,14)

$n=9$, 14 circles: (9,17) (8,18) (5,17) (6,16) (7,19) (7,15) (6,18) (7,17) (8,16)

$n=11$, 30 circles: (5,27) (41,29) (29,37) (44,40) (35,33) (19,35) (35,7) (23,28) (35,37) (30,32) (17,19)

$n=12$, 43 circles: (27,7) (33,5) (37,17) (27,47) (21,5) (32,7) (12,17) (27,22) (42,17) (27,2) (17,17) (22,7)

Here are the questions I want answered:

1. Can you improve any of these solutions? You can use either integer or non-integer coordinates.
2. Can we construct any upper/lower bounds on the maximum number of circles possible for an arbitrary $n$?
3. The solutions for $n$=8, 10 and 12 use two concentric polygons. Can we conjecture that for even $n \geq 8$ the best solution will use two concentric $(n/2)$-polygons?
4. For $n=13$ my best solution uses 43 circles, which is exactly like the $n=12$ case. Surely that extra point must be useful for a few more circles?

Answer 1

A simple upper bound:

Since three points in the plane determine a circle any two distinct circles cannot have a triplet in common. We thus get an upper bound by counting all triplets and dividing by the number of triplets in a quadruplet $\left\lfloor\frac{\begin{pmatrix} n \\ 3 \end{pmatrix}}{\begin{pmatrix} 4 \\ 3 \end{pmatrix}}\right\rfloor=\left\lfloor\frac{\begin{pmatrix} n \\ 3 \end{pmatrix}}{4}\right\rfloor=\left\lfloor\frac{n(n-1)(n-2)}{24}\right\rfloor$

This evaluates to $n=7 \rightarrow 8;n=8 \rightarrow 14;n=9 \rightarrow 21;n=11 \rightarrow 41;n=12 \rightarrow 55$

A simple lower bound:

Construction: n even: 2 concentric parallel regular n/2-gons. This creates lots of trapezia with two points in either n/2-gon each permitting a circle. For n odd we can add the center point and use the same construction for n-1. IF (n-1)/2 is odd we can place the parallel sides of the (n-1)/2-gons opposite to each other and adjust the sizes of the two (n-1)/2-gons to create (n-1)/2 more circles all passing through the center, 2 points of the smaller (n-1)/2-gon and one point of the larger one. We can make a similar construction for (n-1)/2 even by rotating one (n-1)/2-gon so its corners align with the centers of the sides of the other. Also, note that if four points happen to be collinear we can still count them because we can use inversion in a circle centered at a point in general position to transform all such straight lines into proper circles.

Counting circles yields $2 + \frac {(n-1)[(n-1)(n-5)+16]} {32}$ for $n\equiv 1 \mod 4;n\ge9\ $,$\ 2 + \frac {(n-1)[(n-3)^2+16]} {32}$ for $n\equiv 3 \mod 4;n\ge11\ $,$\ 2 + \frac {n[(n-2)^2+4]} {32}$ for $n\equiv 0 \mod 4;n\ge8$ and $2 + \frac {n(n-2)^2} {32}$ for $n\equiv 2 \mod 4;n\ge10$

This evaluates to $n=8 \rightarrow 12;n=9 \rightarrow 14;n=11 \rightarrow 27;n=12 \rightarrow 41$

The lower bound constuction for $n=13$ beats OP by a single cirlce:

The full configuration (bottom right panel) is obtained as 3 rotated overlays of the two templates (top right and bottom left panels, 6 circles each) plus the circumcircles of the two hexagons and six circles through the center (top left panel) for a total of 44.

Lower bound at $n=14$:

The full configuration (right panel) is obtained as 7 rotated overlays of the template (left panel, 9 circles each) plus the circumcircles of the two heptagons for a total of 65.

Answer 2

14 trees with 73 circles (remove B or I to form a solution for 13 trees with 53 circles)

1:A=(-1.2208577248401677090604559983157963834, -3.1468480523080114886881271169977579250)
2:B=(-1.9478233124221029597568335446233091471, -1.9030657422906829627855358303024612249)
3:C=(-2.7527647907411112446780188831961624579, -3.5363463784316339145936381145450808675)
4:D=(-0.82783248947524419914841475107311902588, -0.80881034795529151745796572847987162035)
5:E=(0.73831734921240420520581932243142318234, 1.9030657422906829627855358303024612258)
6:F=(1,0)
7:G=(-1.8691742383633934665857228826763170467, 0)
8:H=(-1.5323609202837326010799277620171050618, -1.6348501262607572224466639246140796226)
9:I=(-1.9854399388298223415753940842379802469, -2.8132724283050665407238088353110992720)
10:J=(-2.2258288971159533487712352984471172569, -1.4274195298222514843054347812245927651)
11:K=(1.3430703308172535824813264335273661652, -2.4949510095897986824206185955346039503)
12:L=(-0.52723171215234560757205083333012202590, 0.97941058062225676502940186295657279032)
13:M=(0,0)
14:N=infinty

4 consecutive letters forms a circle, such as circle ABEG,ABHI, etc

ABEGABHIABJNABKMACDGACEFACHJACKNACLMADHKADIJADLNAEHLAEIKAEMNAFHMAFILAFJKAGHNAGIMAGJLBCDFBCHKBCIJBCLNBDHLBDIKBDMNBEHMBEILBEJKBFHNBFIMBFJLBGINBGJMBGKLCDHMCDILCDJKCEHNCEIMCEJLCFINCFJMCFKLCGHICGJNCGKMDEFGDEINDEJMDEKLDFHIDFJNDFKMDGHJDGKNDGLMEFHJEFKNEFLMEGHKEGIJEGLNFGHLFGIKFGMNHILNHJKNHJLMIJKMKLMN

And another one with different parameters after circle inverse transformation where all black circles are same pattern as that in the bicenter regular polygons while red circles are extra circles.

https://github.com/emathgroup/selectedTopics/blob/master/content/attached/files/c14.html is the geogebra version of it and you could change parameters (o,d and point NN) freedomly.

Similarly 15 trees could have 90 circles and 16 trees 120 circles: https://github.com/emathgroup/selectedTopics/blob/master/content/attached/files/c16.html

And it seems: if $n \equiv 0\pmod 4$, $\text{A337747}(n)=\frac{n((n-2)^2+ 4)}{32}+2×\text{A008610}(\frac{n}2-3)$ if $n \equiv 2\pmod 4$, $\text{A337747}(n)=\frac{n(n-2)^2}{32}+2×\text{A008610}(\frac{n}2-3)$

Answer 3

I rewrote my solver so it is smarter and can handle non-integer coordinates. I have managed to improve $n=12$:

I can get 45 circles with (1.551724138, 2.379310345) (3, 3) (-1, -1) (0, 1) (0.729729730, 1.378378378) (1.153846154, 1.769230769) (0.931034483, 2.172413793) (0.333333333, 1.666666666) (2.2, 1.4) (0.529411765, 0.882352941) (1.153846154, 0.230769231) (1.615384615, 1.923076923). I am not sure if this solution is possible with integer coordinates.

I also improved $n=13$:

I can get 47 circles. Surprisingly there is no obvious symmetry in this solution: (1.153846154,0.769230769) (3,4) (2.6,3.2) (2,1) (4.2,1.6) (1.551724138,1.379310345) (1,0) (3,2) (1,2) (3,1) (1.975609756,0.780487805) (2.846153846,1.230769231) (0.529411765,1.882352941)

I made a small improvement to $n=15$:

I can get 73 circles: (1.411764706, 1.352941176) (0.6, 2.2) (2.04, 0.72) (2.12, 0.84) (3.6, 0.2) (5, 1) (1.846153846, 0.769230769) (0.705882353, 1.823529412) (1.294117647, 1.176470588) (3.2, -0.4) (2, 1) (3, -2) (0.588235294, 1.647058824) (1.216216216, 1.297297297) (0.2, 1.6)

Answer 4

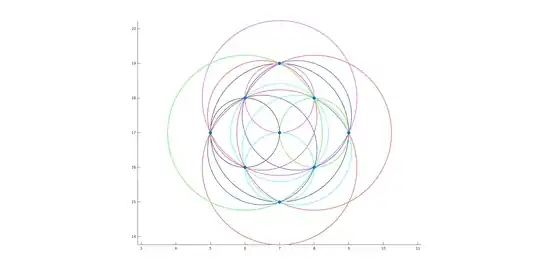
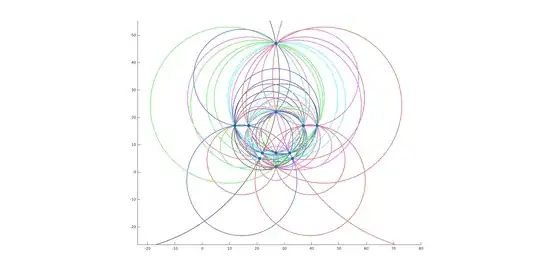
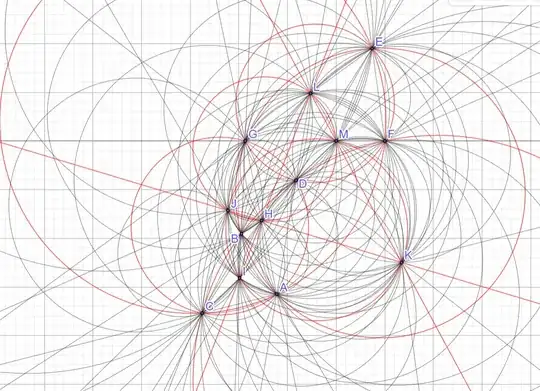
For n=9, there're four groups of different solutions with 14 circles: One candidate is infinity point + (0,0), (1,0), (0.5, 1.3228756555322952952508078768196302129), (-0.25,0.66143782776614764762540393840981510643) (2.5,1.3228756555322952952508078768196302129), (-1,0), (-1.5,1.3228756555322952952508078768196302129), (-0.5,-1.3228756555322952952508078768196302129) where 1.3228756555322952952508078768196302129 is $\frac{\sqrt{7}}2$

All available solutions could be got from equations:

sd8/f484.7.out  
      _[1]=4d2-7  
      _[2]=k+1/2  
      _[3]=c-1/2  
      _[4]=b+d  
      _[5]=a-3/2  
sd8/f4041.7.out  
      _[1]=4d-1  
      _[2]=k+1/2  
      _[3]=c-1/2  
      _[4]=b+d  
      _[5]=a-3/4  
or  
      _[1]=4d+1  
      _[2]=k+1/2  
      _[3]=c-1/2  
      _[4]=b+d  
      _[5]=a-3/4  
sd8/f13492.7.out
      _[1]=16d2-7
      _[2]=k+1/2
      _[3]=c-1/4
      _[4]=b+d
      _[5]=a-1/4
sd8/f12577.7.out  
      _[1]=c4k2+2c2d2k2+d4k2+c4k+2c2d2k+d4k-2c3k2-2cd2k2-c2k3-d2k3+c4+2c2d2+d4-2c3k-2cd2k-2c2k2-2d2k2+2ck3-2c3-2cd2-c2k-d2k+4ck2+c2+d2+2ck  
      _[2]=-2c3dk4-2cd3k4-c2dk5+4bd2k5-d3k5+bk7-4c3dk3-4cd3k3+8bd2k4-4d3k4+2cdk5+2bk6-6c3dk2-6cd3k2+12bd2k3-8d3k3+6cdk4+bk5-dk5-4c3dk-4cd3k+3c2dk2+8bd2k2-9d3k2+10cdk3-dk4-2c3d-2cd3+2c2dk+4bd2k-6d3k+8cdk2+2c2d-2d3+4cdk  
      _[3]=2c3dk3+2cd3k3+c2dk4-4bd2k4+d3k4-bk6+4c3dk2+4cd3k2-8bd2k3+4d3k3-2cdk4-2bk5+4c3dk+4cd3k-c2dk2-8bd2k2+7d3k2-6cdk3+dk4+2c3d+2cd3-2c2dk-4bd2k+6d3k-8cdk2+bk3+dk3-c2d+3d3+2bck-4cdk-2bk2-dk2-2cd-2bk+2d  
      _[4]=c4dk+2c2d3k+d5k+2bc3k2+2bcd2k2-bc2k3-bd2k3+bc4+2bc2d2+bd4-4c3dk-4cd3k-4bc2k2-c2dk2-d3k2+bk4-2bc3-2bcd2-bc2k+4c2dk-bd2k+2bck2+2cdk2+bk3+bc2+bd2+2bck-bk2-dk2-bk+d  
      _[5]=c3k2+cd2k2+c2k3-2bdk3+d2k3+ak4+c3k+cd2k-2bdk2+2d2k2+ak3-2ck3-k4+c3+cd2-2bdk+2d2k-3ck2-k3-c2+d2-2ck  
      _[6]=c2dk+d3k+2bck2-bk3+bc2+bd2-2cdk-2bk2-bc+ad-bk+dk  
      _[7]=ack-c2k+bdk-d2k-ak2-c2-d2-ak+ck+k2+c+k  
      _[8]=c3k+cd2k+c2k2-2bdk2+d2k2+ak3+ac2+ad2-c2k+d2k-2ck2-k3-ac-bd-ak-ck+k  
      _[9]=a2k+b2k-c2-d2-2ak+2c+k  
      _[10]=a2c+b2c-ac2+c3-ad2+cd2+c2k-2bdk+d2k+ak2-a2-b2+ac-2c2+bd-ak-2ck-k2+c+k+1  

(I have thought there should be no real roots of the last equation, but in fact we could find infinity number of real roots).

For any solution of the above equations, We need to find a real projective transformation to transform complex point (a+bi, c+di) to infinity points (1:i:0),(1:-i:0).

The projective transformation will transform 8 points (0,0), (1,0),(0,1),((1+k)/k,1),(1,k+1), (1:0:0),(1:k:0),(0:1:0) into a result (Add an extra infinity point) For example, if k=-1/2;a=1,b=1,c=3/10,d=-1/10; The 8 points could be projected to (0,0),(1,0),(1,2),(9/5,12/5),(0,3),(-3,0),(3/2,3/2),(3/5,6/5)

I have verified that for n=9, there're at most 14 circles and for n=10, there're at most 22 circles too.

Answer 5

For n=11, there're at most 30 circles. One group of the solution for 30 circles are find real number a and t so that real number $b^2=\frac{((-4*a^3 + 20*a^2 - 32*a + 16)*t^2 + (2*a^3 - 10*a^2 + 16*a - 8)*t + (a^2 - 2*a + 1))}{((4*a - 4)*t^2 + (-2*a + 2)*t - 1)}$ $c=t,d=\frac{(2*b*c^2 - 2*b*c)}{-((2*a - 4)*c + 1)}$ Find the projective transformation to tranform (a+bi,c+di) to infinity point (1:i:0) and (a-bi,c-di) to infinity point (1:-i:0). Apply the transformation above to 10 points

"list n1=1,0,0;\n"//A, 
"list n2=1,0,1;\n"//B
"list n3=(1-4t),2t(1-2t),(1-2t);\n"//C
"list n4=0,1,1;\n"//D
"list n5=0,0,1;\n"//E
"list n6=2,2t,1;\n"//F
"list n7=0,1,0;\n"//G
"list n8=2,2t-1,0;\n"//H
"list n9=2,2t-1,1;\n"//I
"list n10=1,t,1;\n";//J

and include infinity points we could get 11 points with 30 circles. (12 of them are straight lines) such as a=1/3, t=0.22,b=0.11908559882815065066807104006502303474,c=0.22, d=0.1532631656918298874098074285636846457 The matrix for the projective transformation is [-1 1.2739641311069882498453927025355596784 0] [0 -0.34620989492339901594966107566213561308 0] [-1.1938775510204081632653061224489795919 0.92764378478664192949907235621521335802 0.19387755102040816326530612244897959185]

45 circles are also best result for 12 trees CGHLDEFLCFJLCEKLFHILEGILDGJLDHKLIJKLACILBDILBEJLBFKLAHJLAGKLABCDABEHABFGACEGACFHACJKADEKADFJADGHAEFIAGIJAHIKBCEFBCGJBCHKBDEGBDFHBDJKBEIKBFIJBGHICDEHCDFGCEIJCFIKDGIKDHIJEFGHEGJKFHJK

si[1]=bc-ad-bt-dt+b
si[2]=ac+c2+bd+d2-at-ct+a+t-1
si[3]=a2+b2-c2-d2+2at+2ct-2a-2t+1
si[4]=2c2d+2d3-4adt-4cdt-bt2-dt2+4ad+3bt+5dt-2b-2d
si[5]=2c3+2cd2-2c2t+4bdt+2d2t-at2-ct2-2c2-4bd-2d2+3at+5ct+t2-2a-2c-3t+2
si[6]=4b2dt+4bd2t-abt2+cdt2-bt3-dt3-4b2d+3abt+4adt+cdt+5bt2+2dt2-2ab-2ad-8bt-3dt+4b
si[7]=4abdt+4ad2t+b2t2+4bdt2+3d2t2-4abd-3b2t-8bdt-d2t+2b2+2bd
ring r1=0,(a,b,c,d,t),dp;
list n1=1,1,1;
list n2=-1/2*t + 1/2,1/2*t,1;
list n3=0,1,0;
list n4=-t,t,1;
list n5=-t + 1,t - 1,1;
list n6=0,0,1;
list n7=t,-t + 1,0;
list n8=1,0,0;
list n9=1,0,1;
list n10=0,1,1;
list n11=-t + 1,t,1;

and Geogebra dynamic graph for it at https://github.com/emathgroup/selectedTopics/blob/master/content/attached/files/c12.ggb