4

When you really want to tile more than one layer but triple tiling is just too much of a good thing, surely the happy medium is double tiling.

  • How may a mosaic of more than 900 sections be double tiled with congruent triangles along the 6 guidelines listed below?

Here are two examples of double tiling with congruent triangles. The first example demonstrates most guidelines of this puzzle while the second follows the toughest guidelines as well.

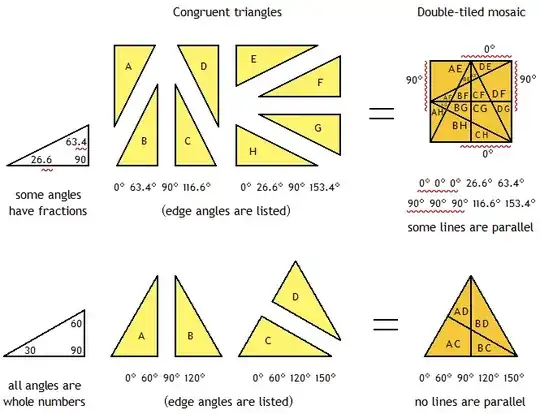
In the first example, eight overlapping 26.6°- 63.4°- 90° triangles double tile a square mosaic of 15 sections where:

  1. “Double tiling” is taken to mean that every section of a mosaic is completely covered by portions of exactly two tiles and that all tiles lay completely within that mosaic.

  2. The tiles are congruent triangles.

  3. Each tile is uniquely oriented.

  4. The mosaic is edge-contiguous in that all sections may be visited along a single unbroken path that stays within the mosaic while crossing tile edges from section to section without touching any vertex.

In the second example, four overlapping congruent 30°- 60°- 90° triangles double tile a triangular mosaic of 4 sections where, moreover:

  1. Every angle is a whole number of degrees.

  2. No distinct lines are parallel. (Parallel tile edges may, however, lie along a single continuous line.)

Bounty challenges, achievability unknown

  • Double tile a mosaic other than the second example above that follows all 6 guidelines and has no holes.

  • Double tile a mosaic that follows all 6 guidelines and whose outline is not bilaterally symmetric.

(All interesting double tilings, including those with fewer than 901 sections and/or those that disregard some of the above guidelines, deserve votes of approval.)

humn
  • 21,899
  • 4
  • 60
  • 161
  • 1
    Do all answers have to adhere to all 6 rules? I managed to work out some interesting results satisfying the first 5 and am hesitating whether to post them. – iBug Aug 17 '20 at 12:52
  • The puzzle statement now encourages posting of interesting double tilings that don't follow a listed guideline or two – humn Sep 13 '20 at 19:52

2 Answers2

2

I have a hunch the intended solution may be something like

enter image description here That's a 45-gram, 45 being the largest odd number still allowing for integer angles. Odd to avoid parallel lines. By maximally twisting the 45-gramm i.e. by choosing the one with the maximal number of full turns (22) we maximise the number of sections each tile splits into (21) for a total of just above 900. The entire figure by construction has no parallel lines. The two tilings are obtained by rotating the triangle around the center (in particular, all are congruent and oriented differently) and by mirroring. Edge-continuity is also easy to verify since we have everything except the innermost ring and the territory outside the two outermost rings of intersection points to freely move around. Please blame OP if you find the picture too visually busy ;-D

For better clarity here are a few smaller examples:

enter image description here n=7: not edge continuous, non integer angles, (n-3)/2 = 2 sections per tile enter image description here n=9: not edge continuous, integer angles, (n-3)/2 = 3 sections per tile enter image description here n=11: edge continuous, non integer angles, (n-3)/2 = 4 sections per tile

Paul Panzer
  • 10,341
  • 18
  • 48
  • OP passes blame to the 360 degrees in a circle. Before post time a trial solution had only 14 sections, with non-integer angles. Feel free to use something like that to show how your solution works, @Paul Panzer, and congratulations for zeroing in on the essence of what makes your solution maximal. – humn Sep 14 '20 at 22:00
1

(Community wiki – feel free to add or edit.)

In lieu of hints from puzzle’s poser here are a couple of almost-solutions that follow most guidelines but not all. Ten congruent 36°- 72°- 72° triangles double tile a contiguous mosaic of 10 sections but the triangles are not uniquely oriented and the mosaic has 5 pairs of parallel lines:

Twelve uniquely oriented congruent 30°- 60°- 90° triangles double tile a contiguous 12-section mosaic that yet includes 6 pairs of parallel lines:

humn
  • 21,899
  • 4
  • 60
  • 161