2

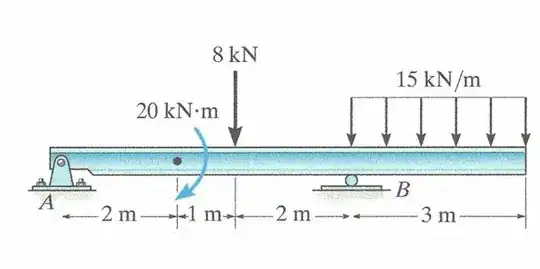
enter image description here

Consider the beam in the picture above. There are several forces that cause moments around all points in the beams. But there is also one "explicit" moment: 20kNm.

How do I interpret these kinds of moments? Here the arrow goes around the point 2m from A. So does this mean there is an extra moment around this point? But how does this moment affect the moment seen from other points, such as A? Or B? More specifically, if I wanted to form a moment equilibrium equation from A, would I simply add/subtract (depending on my definition of positive direction) 20kNm from/to the sum of moments about A? And if I were to form moment equilibrium equations around another point like B, what would I do with 20kNm then? Also, how would this kind of moment occur in real world? It is a moment without a force or a distance, just a moment. How could I produce something like this? Thank you!

This is not a homework question; I am currently taking a course on statics but this specific example is one I found somewhere that illustrates my problem.

S. Rotos
  • 903
  • Think of it as 2 forces of 10kN, each 1 meter from the dot, one to the right that is down ad the other to the left that is up. That way you have get the torque at 20kN but the force summation is 0. – PhysicsDave Mar 14 '19 at 22:59
  • You really ought to include the whole of the question, or the part of the textbook which explains the diagram. – sammy gerbil Mar 14 '19 at 23:15
  • The "explicit" moment requires no more interpretation than the $15\ \mathrm{kN/m}$ force field. Just compute! Theres nothing mysterious going on there. – Gert Mar 14 '19 at 23:39
  • @sammygerbil Why? The OP is just interested in the diagram, and I don't see any reason to say where it is from. – BioPhysicist Mar 15 '19 at 00:17
  • @AaronStevens Diagrams are usually explained in the texts in which they are printed. – sammy gerbil Mar 15 '19 at 00:25
  • @sammygerbil Right, but I don't see why it's needed here. – BioPhysicist Mar 15 '19 at 00:33
  • @AaronStevens The text will answer the question. It is the ideal source for interpreting the diagram. – sammy gerbil Mar 15 '19 at 00:35
  • @sammygerbil The OP's issue isn't with understanding the diagram. They know there is a moment at the specified location. They are asking about the physics and how it relates to the system. Although I will agree that the answer could probably be obtained by studying the text, but I don't think they will find that answer just in a diagram description. – BioPhysicist Mar 15 '19 at 00:52
  • @AaronStevens The questions in the OP's 2nd paragraph do relate to the interpretation of the moments in the diagram, and the inter-relation between them. The textbook would explain how such diagrams are to be interpreted.. – sammy gerbil Mar 15 '19 at 16:30
  • I have revised my answer to address your specific questions. Hope it helps – Bob D Mar 15 '19 at 19:46
  • @Gert 15 kN/m is a distributed load. Not sure what you mean by a "force field". And the 15 kN/m distributed load has nothing to do with the 20 kN/m force couple. – Bob D Mar 15 '19 at 21:40
  • 1
    @sammygerbil There is no reason to include the textbook explanation of the diagram. The dot with the curved arrow and value of 20 kN/m tells anyone who knows statics that it represents a force couple, as described by PhysicsDave. – Bob D Mar 15 '19 at 21:43
  • @BobD: distributed load = force field. Synonyms. – Gert Mar 15 '19 at 21:45
  • 1
    @AaronStevens You are right there is no need to explain this diagram. It is clear to anyone knowing statics that 20 kN/m is a force couple. – Bob D Mar 15 '19 at 21:46
  • @Gert OK that's a new one on me. But it still has nothing to do with the 20 kN/m force couple. – Bob D Mar 15 '19 at 21:47
  • @Gert Could you please direct me to where a distributed load on a beam is a force field? It would further my education. Thanks – Bob D Mar 15 '19 at 21:50
  • @BobD: you're making too much of this. Where I'm from that kind of load ($15\ \mathrm{kN/m}$) is also known as a homogenous force field. It's just an expression. Call it a distributed force by all means. – Gert Mar 15 '19 at 21:53
  • @Gert Sorry Gert but I wasn't trying to make too much of it. A force field, to me, is like a gravitational field or electrostatic field that exerts a force on mass or charge, respectively. I was more concerned about the idea that there was some kind of connection between the 15 kN/m (force field or distributed load) and the 20 kN/m force couple. But let's leave it there. – Bob D Mar 15 '19 at 21:58

3 Answers3

2

How do I interpret these kinds of moments?

The 20 kN.m moment is called a "couple" or “force couple”. A force couple is produced by equal and opposite parallel forces (net force = 0) about a point at the center between them. A couple causes pure rotation without translation.

A couple has the following properties:

  1. It is equivalent to a single moment vector.

  2. It induces the potential for rotation without translation (because for equal and opposite forces there is no net force)

  3. In order to achieve equilibrium for the entire beam, a couple can only be counteracted by another equal and opposite couple.

  4. The moment vector of the couple and be moved to any location without affecting static equilibrium requirements.

ADDENDUM

The following are answers to your specific questions. They assume you are only considering static equilibrium requirements for the beam, because the fourth property only applies to statics analysis (e.g.,. setting the sum of the forces and moments equal to zero to determine reactions at supports). For mechanics of materials problems, the location of the force couple is critical to determine bending moments and bending stresses.

Here the arrow goes around the point 2m from A. So does this mean there is an extra moment around this point?

Yes. But you don’t have to take the point where the couple is located into consideration because of the fourth property. You only need to take the location of the couple into consideration when you are determining bending moments and stresses in the beam, in other words, for mechanics of materials problems. For statics problems, where you are only trying to determine reactions at supports for static equilibrium, the location of the couple is unimportant.

But how does this moment affect the moment seen from other points, such as A? Or B? More specifically, if I wanted to form a moment equilibrium equation from A, would I simply add/subtract (depending on my definition of positive direction) 20kNm from/to the sum of moments about A?) And if I were to form moment equilibrium equations around another point like B, what would I do with 20kNm then?

If you want to sum moments about A, you can think of the couple being located at A and just add/subtract it to the other moments about A.

If you want to sum moments about B, you can think of the couple being located at B and just add/subtract it to the other moments about B.

You get the same results either way.

REMEMBER- This only applies to static equilibrium requirements. When you analyze bending moments and stresses in beams the couple location is critical;.

Also, how would this kind of moment occur in real world? It is a moment without a force or a distance, just a moment. How could I produce something like this? Thank you!

This is not a moment without a force. It is moment caused by two parallel equal and opposite forces. So it is a moment without a net force.

Think about the steering wheel of your car. To make a right hand turn, you exert a vertical upward force with your left hand and an equal and parallel downward vertical force with your right hand. Because your forces are equal, parallel, and opposite, you are creating a moment couple on the wheel. That is, you create a torque (moment) about the center of the steering wheel without any net force on the wheel.

The following link from an MIT site describes couples in more detail and gives examples (such as the steering wheel), including one involving a bridge.

http://web.mit.edu/4.441/1_lectures/1_lecture12/1_lecture12.html

Hope this helps.

Bob D
  • 71,527
2

Realizing that accepting my previous answer would be based on you accepting and understanding the definition and properties of couples, the following is intended to help in that regard.

Definition of a couple:

A moment created by two equal, opposite and parallel non-collinear forces.

Fig 1 below is an example of a couple. The net force is zero. Each force causes a clockwise moment about the point in the center equal to $\frac {Fd}{2}$ for a total moment of $Fd$. Note that the magnitude of the couple is the same if larger forces are closer together or smaller forces are further apart. For this reason showing the forces is unnecessary and the symbol to the right of the example is often used.

1. It is equivalent to a single moment vector.

The symbol of the couple reflects this property. For a couple formed by forces in the x-y, by the right hand rule a counter clockwise couple vector is in the positive z direction and is typically indicated as positive.

2. It induces the potential for rotation without translation.

This is evident from Fig 1. There is no net force.

3. In order to achieve equilibrium for the entire beam, a couple can only be counteracted by another equal and opposite couple.

To illustrate this property, consider the simply supported beam of Fig 2A. A single force couple is applied to the center of the beam. The static equilibrium requirements are the sum of the forces and sum of the moments are zero.

Summing the forces we obtain $R_{A}=-R_{B}$. The reaction forces are equal, opposite and parallel to each other. Therefore they form a couple.

Summing the moments we get $R_{A}=-F/2$ and $R_{B}= +F/2$. Therefore the couple formed by the reactions is counter clockwise, countering the applied couple.

4. The moment vector of the couple can be moved to any location without affecting static equilibrium requirements.

Note that the location of the applied couple (point C) in Fig 2 had no influence on the sum of the forces for equilibrium. No matter where it is, the reactions will be equal and opposite.

Likewise, the location of C will have no influence on the sum of the moments for equilibrium. For example, in Fig 3 the location of the couple, point C, has been moved so that it is now $L/4$ to the right of A instead of in the center. The sum of the moments about A remains zero.

Hope this helps. enter image description here

Bob D
  • 71,527
  • Thank you - that clears it up! – S. Rotos Mar 17 '19 at 13:53
  • Does this reasoning still apply when interested in internal forces, i.e. shear forces and bending moments? I figure that converting the "explicit" moment into an "equivalent" force couple produces different shear force diagrams and bending moment diagrams. I witnessed this when playing around with SkyCiv (skyciv.com). Edit: I've noticed you mentioned this in your other answer. So, how do you treat the "explicit" moment when dealing with internal forces? Is it only valid to sum moments at the point where the "explicit" moment is defined? – Kcronix Jun 11 '19 at 09:15
  • @Kcronix Instead of "explicit moment" the proper term is a couple or pure moment. Moving a couple or replacing it with equivalent force couples does not affect static equilibrium requirements (e.g., reactions at supports). But it will produce different shear and bending moment diagrams as you say. So when doing shear and bending moment diagrams, leave them alone. Hope this helps. – Bob D Jun 11 '19 at 12:23
  • @Kcronix I should add, however, that you can move a couple without affecting the shear diagram. There is no change in shear force due to a couple. That's because for a couple there is no net force. – Bob D Jun 11 '19 at 14:45
0

I am very much aware that this thread has been a while but I am sure people keep coming here. If we look into the Euler-Bernoulli equation, this explicit moment is actually an imposed boundary condition (BC): the third derivative of the deflection wrt its horizontal axis (the x-axis).

In an Euler-Bernoulli, the input is only force/pressure. We can't apply torque. Hence, this explicit torque is a given BC for us to use as we solve the Euler-Bernoulli equation. If we perform a finite difference discretization, it is indeed a force couple but these force couple are not equal.

manurunga
  • 29