0

Initially it seemed to me that falsificationism is a reliable scientific methodology for disregarding hypotheses/theories. Upon some thinking, however, I conclude that it is not. Below I explain why. Can you give me your thoughts on this?

Falsification of a hypothesis appears to be be possible by extrapolating a prediction from a hypothesis which, given a particular set of observations/cases/experiments, is false - seemingly making the hypothesis false as well.

is a universal hypothesis which states that object 'x', when existing in condition 'W' behaves in 'Z' manner.

We observe a particular set of 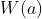and 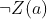hence .

Logically this can be represented as:

thus

To make things simple let's simplify above by the following:

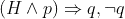
thus

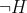
Now, algebraically via Morgans law if we apply a negation to both sides of implication where the left side is a conjunction (we are doing that in order to achieve negation of q) we get:

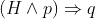
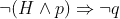
which is equivalent to

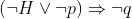
This means that observation of 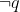does not entitle us to conclude that 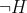is the case, as we have logical disjunction on the left side!

I am puzzled by that. Basically even if you observe a negation of prediction made from hypothesis it doesn't mean that the hypothesis is false. It could be that the observation itself is false. As a scientist it makes me a bit uncomfortable...

--- BELOW ADDED FOR CLARIFICATION (in the light of comments)

I have relied on in my proof because scientific prediction is never made directly from hypothesis. Instead it is made from 'instantiation' of hypothesis, which could be in form of e.g. observation or designed experiment. Let me illustrate by example.

Let 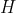be "Glass breaks when thrown on the floor". Now we design the experiment in an attempt to falsify 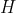. Let 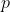be "I design experiment where I throw a piece of glass on the floor". 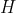survives the falsification attempt when 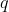is "I see glass breaks". However it doesn't. Thus negation of 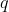is the case. According to the proof presented above it is not possible to falsify 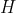with this observation.

My question is whether there is a sound philosophical answer to this conundrum that is hand-in-hand with falsifiability.

curious_bitcoiner
  • 1
  • 1
  • I'm not following your logic completely, but I think you might have stumbled upon Hempel's paradox. – Alexander S King Mar 09 '17 at 20:15
  • That being said, Falsificationism faces bigger problems than Hempel's Paradox. See Kuhn, Quine, and Feyerabend. – Alexander S King Mar 09 '17 at 20:19
  • 1
    The "logical" steps are quite confusing... but the argument is sound. The Discovery of Neptune followed exactly this pattern: instead of leaving the seemingly confuted Law of Gravitation, Le Verrier predicted the existence of a new unobserved planet. In a certain sense, the "observed fact" regarding the number of planets was discarded in place of the general hypothesis. – Mauro ALLEGRANZA Mar 09 '17 at 21:13
  • 1
    Observations are statistical and assume ceteris paribus clauses, so yes, observation (interpreted as) ¬q can be "false". I think the problem you are pointing out relates to the inversion of conditional probabilities in significance testing: estimated is not the probability of the hypothesis given the data, but rather the probability of the data given the hypothesis. This is indeed criticized, but alternatives (like Bayesianism) are not exactly better, see Fisher vs. Popper vs. Bayes. – Conifold Mar 09 '17 at 21:58
  • When you replace W(x) with H^p, it's not clear what H and p represent. This looks like Duhem's argument in La théorie physique [trans. as The Aim and Structure of Physical Theory]: When we test a hypothesis H, we typically rely on a set of other assumptions (about how our instruments are working, that nothing's interfering with the experiment, etc.), p. The conjunction H^p implies the expected observation q. So when we observe not-q, we can't conclude not-H. See SEPh article on underdetermination: https://plato.stanford.edu/entries/scientific-underdetermination/#FirLooDuhQuiProUnd. – Dan Hicks Mar 09 '17 at 23:35
  • For me, all of the latex typeset images are broken. – Dave Mar 10 '17 at 18:54

1 Answers1

1

The meat of your question is here:

Initially it seemed to me that falsificationism is a reliable scientific methodology for disregarding hypotheses/theories. Upon some thinking, however, I conclude that it is not. Below I explain why. Can you give me your thoughts on this?

Falsification of a hypothesis appears to be be possible by extrapolating a prediction from a hypothesis which, given a particular set of observations/cases/experiments, is false - seemingly making the hypothesis false as well.

...

Basically even if you observe a negation of prediction made from hypothesis it doesn't mean that the hypothesis is false. It could be that the observation itself is false. As a scientist it makes me a bit uncomfortable...

You could have left out most of the rest of what you wrote. For future reference, you should try to write down your ideas in plain English whenever possible. Maths and logical formalism are more useful for testing ideas than stating them.

Falsificationism is not the name of a position held or advocated by anyone. It is, rather, a label used to straw man Karl Popper's positions rather than take them seriously. Looking it up is a fool's errand and will result in you reading low quality philosophers like Kuhn or Feyerabend who can't even state ideas correctly never mind refute them. There is also a cottage industry of commentary on such low quality philosophers who are cited everywhere while the refutations of their ideas given by Popper (such as the title essay of 'The Myth of the Framework') and other competent people are ignored.

The way knowledge is actually created in science was explained by Karl Popper. You notice a problem with a current theory: something it doesn't explain like an experimental result, or a clash with another theory or whatever. You guess solutions to that problem. Then you criticise the guesses by experiment, or looking for clashes with other ideas. You keep doing this until there is only one remaining theory and it has no known criticisms. Then you have solved the problem and move on to a new problem. All scientific knowledge consists of guesses controlled by criticism.

Now, suppose you have done an experiment. The result of the experiment is a guess about what happened in some particular place and time. That guess involves explanations of how the experimental apparatus works and that sort of thing. Your guess about the result of that experiment could be wrong. So you look for problems with the result. If you find such problems and fail to solve them then you might guess the experimental result is wrong and should be discarded. You then look for some new way of testing the theory the experiment was intended to test. If you haven't found a problem with the experimental result, and the result of the experiment is inconsistent with the theory it was intended to test, then that theory has an unanswered criticism and should be modified or abandoned.

For more detailed explanations, see "The Fabric of Reality" by David Deutsch, Chapters 3 and 7, "The Beginning of Infinity" by Deutsch, Chapters 1 and 2, "Realism and the Aim of Science" by Popper Chapter I, "Objective Knowledge" by Popper chapter 1.

alanf
  • 7,748
  • 13
  • 20
  • You're right that logical formalism is useful for testing ideas. That's exactly what I wanted to accomplish in my post. I think presented formalism very elegantly shows the problem with core methodology of falsificationism. I disagree with you in terms of the usage of falsificationism, as there is plenty of literature where it is used for serious philosophical analyses, e.g. Polish author Adam Grobler uses the term in his Methodologia Nauk ( "The Methodology of Sciences", my translation of title). – curious_bitcoiner Mar 10 '17 at 14:46
  • What you outlined seems like a common sense everyday business of how some scientists do their job. However my question was not about "how to do science" but rather whether there is alternative logical framework for falsificationism that overcomes the presented problem. – curious_bitcoiner Mar 10 '17 at 14:51
  • In relation to what you said, though, you say " You keep doing this until there is only one remaining theory and it has no known criticisms". This seems to be incoherent with falsificationism as all theories are always open to continuous critisism (the same as attempting to falsify them). Also, how can you know that there is a "problem with current theory"? To know that you either have an observation/controlled experiment which shows the theory to be false BUT this is not possible given the logical proof above. You can also substitute observation with other theory. – curious_bitcoiner Mar 10 '17 at 15:01
  • Holding a theory open to criticism is not the same as having an actual known criticism. An observation or controlled experiment is not the only kind of problem, e.g. - there is no known experimental result contradicting quantum theory, but there is still a problem of inventing a quantum theory of gravity. Now, if your current explanation of the result of an experiment contradicts your theory then either your theory is wrong or your explanation of the experiment is wrong. Either way you have a problem to solve. – alanf Mar 10 '17 at 22:35