I'm trying to implement a MINLP problem which is described in a previous post here: How do we formulate a problem where the decision variable has an index that is also a decision variable? The only change is that the objective function is different and is to be minimized instead of to be maximized (the function has changed but is given below for completeness).
The problem is about minimizing a (nonlinear) objective function w.r.t. $x_i$:
$$\min \sum_{i=1}^N f(x_i, s_i, p_i),$$
where $s_i$ and $p_i$ are constants for each $i=1, 2, \dots, N$ and $x_i$ is a decision variable, where $0 \le x_i < 1$. The function $f$ is
$$f(x_i, s_i, p_i) = p_is_i\frac{x_i^{0.135}-(1-x_i)^{0.135}}{0.1975}.$$
We also have a binary variable $y_{ij}$ and a continuous variable $a_j$ where $0 \le a_j < 1$ and $j = 1, 2, 3$.
The constraints are the following:
\begin{align} \beta= \frac{\sum_{i=1}^N x_id_i}{\sum_{i=1}^N d_i},\tag1\label1 \\ \end{align} where $d_i$ is again a constant for each $i=1, 2, \dots, N$ and $\beta$ is a constant where $0 \le \beta < 1$.
\begin{align} \sum_j y_{ij} &= 1 &&\text{for all $i$}, \tag2\label2 \\ -(1 - y_{ij}) \le x_i - a_j &\le 1 - y_{ij} &&\text{for all $i$ and $j$}. \tag3\label3 \end{align}
I'm implementing it in Pyomo as interface and I use mindtpy as a solver. Here is the code I have implemented (note that I split up constraint $3$).
f = lambda x, s, p: ((x**0.135-(1-x)**0.135)/0.1975)*p*s
Beta = 0.96
model = ConcreteModel(name="ORExchangeExample")
model.x = Var(N, bounds=(0.00, 0.9999), initialize = 0.50)
model.a = Var(J, bounds=(0.00, 0.9999), initialize = 0.50)
model.y = Var(N, J, domain=Binary, initialize=0)
def obj_rule(model):
return sum(f(model.x[n], s[n], p[n]) for n in N)
model.obj = Objective(rule=obj_rule, sense=minimize)
def constraint_1(model):
return sum(d[n]model.x[n] for n in N) == Beta(sum(d[n] for n in N))
model.constraint_1= Constraint(rule=constraint_1)
def constraint_2(model, i):
return sum(model.y[i, j] for j in J) == 1
model.constraint_2= Constraint(N, rule=constraint_2)
def constraint_3(model, i, j):
return -(1-model.y[i, j]) <= model.x[i]-model.a[j]
model.constraint_3= Constraint(N, J, rule=constraint_3)
def constraint_4(model, i, j):
return model.x[i]-model.a[j] <= 1-model.y[i, j]
model.constraint_4= Constraint(N, J, rule=constraint_4)
solver.solve(model, tee=True,
mip_solver='glpk',
nlp_solver='ipopt',)
solver.solve(model)
The variable $N$ is a list containing $1, 2 , \dots, N$ and $J$ is also a list $ = [1, 2, 3]$. The constant variables $p, s$ and $d$ are dictionaries with the elements of $N$ as keys and the actual values as values, for example:
p = {1: 19.06, 2: 4.0607, 3: 9.75, 4: 0.2716, ...}
When I run this, it runs without errors but gives me back as a solution the initialized values for $x$ and $a$. So it doesn't solve it, because constraint (1) isn't met and the objective function is definitely not minimized. The result (in this code set up) will give [0.5, 0.5, ...] for all values of $x_i$.
Am I missing something?
EDIT: I used the Ipopt as the nonlinear solver but still the same result. However, if I do it for a small sample ($N = 10$), then it all works fine...
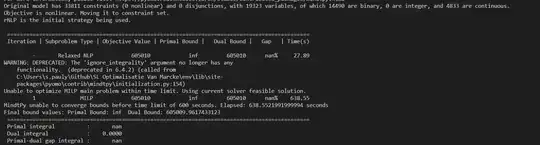
This is what the solver has to say, but I don't really know how to interpret this. In my data, $N = 4831$.