How to partition a giant tour into feasible routes?

Question

In vehicle routing problems, the route first cluster second approach starts by computing a "giant" TSP tour (which typically does not satisfy all constraints of the problem), and then transforms this tour into smaller feasible ones (see for example this paper).

I am wondering if it is possible to apply the same strategy for arc routing problems. A trial and error approach is described here for the CPP, but it is not very satisfying.

Could we formulate a MIP to partition a "giant" eulerian tour into $k$ subtours (with, for example, a maximum length) ? Or is there another smart way of achieving this?

An example is illustrated below:

Answer 1

Here’s a MILP formulation to partition an Eulerian graph into $K$ Eulerian subgraphs, with an objective of minimizing the maximum cost. Let binary decision variable $x_{ijk}$ indicate whether edge $(i,j)$ appears in subgraph $k$, let $y_{vk}$ be a nonnegative integer decision variable for each node $v$ and subgraph $k$, and let decision variable $z$ represent $\max_k \sum_{i,j} c_{ij}x_{ijk}$. The problem is to minimize $z$ subject to contiguity constraints and \begin{align} \sum_k x_{ijk} &= 1 &&\text{for all $(i,j)$} \tag1\label1 \\ \sum_{(i,j):v \in \{i,j\}} x_{ijk} &= 2y_{vk} &&\text{for all $v$ and $k$} \tag2\label2 \\ \sum_{i,j} c_{ij}x_{ijk} &\le z &&\text{for all $k$} \tag3\label3 \end{align} Constraint \eqref{1} assigns each edge to exactly one subgraph. Constraint \eqref{2} forces every node to have even degree in subgraph $k$. Constraint \eqref{3} enforces the minimax objective.

---

Here's a flow-based approach to enforce contiguity of subgraph $k$. Let binary decision variable $w_{ik}$ indicate whether node $i$ appears in subgraph $k$. Let binary decision variable $s_{ik}$ indicate whether node $i$ is the source node for subgraph $k$. Let nonnegative variable $f_{ijk}$ be the flow of "commodity" $k$ from node $i$ to node $j$. The following constraints select one source for each $k$ and send one unit of flow from that source to all other nodes in subgraph $k$: \begin{align} \sum_i s_{ik} &= 1 &&\text{for all $k$} \\ s_{ik} &\le w_{ik} &&\text{for all $i$ and $k$} \\ w_{ik} \le y_{ik} &\le \frac{\text{degree}_i}{2} w_{ik} &&\text{for all $i$ and $k$} \\ f_{ijk} + f_{jik} &\le n x_{ijk} &&\text{for all $(i,j)$ and $k$} \\ \sum_j (f_{ijk} - f_{jik}) &\le n s_{ik} - w_{ik} &&\text{for all $i$ and $k$} \\ \end{align}

---

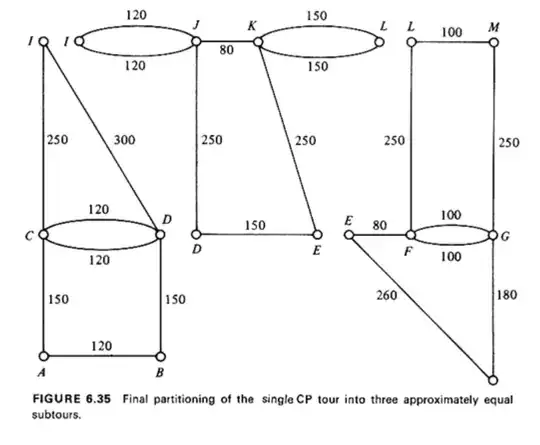
Without the contiguity constraints, the optimal objective value for the example instance with $K=3$ is $1290$, attained by the following subgraphs with weights $1290$, $1270$, and $1240$:

C D 120 
C I 250 
D I 300 
E F  80 
E H 260 
F G 100 
G H 180
A B 120 
A C 150 
B D 150 
C D 120 
D E 150 
D J 250 
E K 250 
J K  80
I J 120 
I J 120 
K L 150 
K L 150 
F G 100 
F L 250 
G M 250 
L M 100 

With the contiguity constraints also imposed, the example solution in the question is optimal, with objective value $1320$.

Answer 2

Here is an alternative to RobPratt's precise solution.

First, compute all simple cycles of the graph $G=(V,A)$ (the graph can be directed in an arbitrary direction). Then, compute $2$-cycles and $3$-cycles, by merging cycles together if they share at least one common vertex (hence guaranteeing contiguity constraints). Let $\Omega$ be the set of all these cycles. The cost of cycle $k$ is denoted by $C_k$.

These cycles are now the variables of the problem, let $x_k \in \{0,1\}$ be a binary variable that takes value $1$ if and only if cycle $k \in \Omega$ is used in the solution. Let decision variable $z$ represent $\max_k \; C_k x_k$. The problem is to minimize $z$ subject to:

• Each edge must be covered exactly once by a given cycle: $$ \sum_{k \in \Omega, (i,j)\in k}x_k =1\quad \forall (i,j) \in A $$
• $z$ is defined as the maximum length of the selected cycles: $$ C_k x_k \le z \quad \forall k \in \Omega $$
• In our case, we can only use $3$ cycles: $$ \sum_{k\in \Omega}x_k = 3 $$

---

Some comments:

1. With the above formulation, I am able to find the optimal solution of the example in the question (in about 2 sec with CBC, and 0.1 sec with CPLEX). A simulation with some (non optimized) code can be found here.
2. The solution is not unique.
3. This is nothing more than a Dantzig-Wolfe decomposition of RobPratt's formulation. The contiguity constraints (and "even degree" constraints) are handled in a pre-processing phase, which makes the model a bit lighter.
4. However, in the general case, computing cycles up to $3$-cycles is not sufficient to guarantee that the optimal solution is reached.
5. One could compute the appropriate cycles dynamically with a column generation procedure (which would complicate the approach quite a bit) and either use branch-and-price (optimal), or solve the restricted master problem once all good columns have been found (heuristic).