Existence of extreme points in primal and dual LP

Question

If the nonempty feasible set of a primal LP has extreme points does its dual also have extreme points? I know that a standard form LP (nonempty) always has extreme points. But I am not sure if we can say anything about dual having extreme points or not given the knowledge that primal LP (standard/general) has extreme points.

Answer 1

Besides useful comment and answer, let's depict out the feasible space of the linear problem and its equivalent dual in some simple examples.

1) When the primal problem has an optimal solution: \begin{array}{l} \text{Maximize} & Z = 3x_1 + 2x_2\\ \text{subject to:}& \\ &x_1 + x_2 \leq 9\\ &3x_1 + x_2 \leq 18\\ &x_1 \leq 7\\ &x_2 \leq 6\\ &x_1,x_2\geq 0, \end{array}

\begin{array}{l} \text{Minimize} & W = 9y_1 + 18y_2 + 7y_3 + 6y_4\\ \text{subject to:}& \\ &y_1 + 3y_2 + y_3 \geq 3\\ &y_1 + y_2 + y_4 \geq 2\\ &y_1,y_2,y_3,y_4\geq 0, \end{array}

The primal and dual feasible spaces would be: 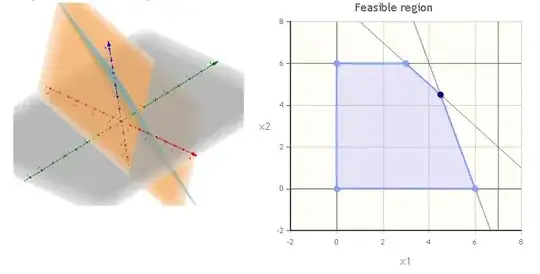Based on the feasible spaces, the primal contains five extreme points and the dual consists of at least one vertex.

2) When the primal does have multiple optimal solutions: \begin{array}{l} \text{Maximize} & Z = x_1 + x_2\\ \text{subject to:}& \\ &x_1 + x_2 \leq 6\\ &-x_1 + 2x_2 \leq 8\\ &x_1,x_2\geq 0, \end{array}

\begin{array}{l} \text{Minimize} & W = 6y_1 + 8y_2\\ \text{subject to:}& \\ &y_1 - y_2 \geq 1\\ &y_1 + 2y_2 \geq 1\\ &y_1, y_2 \geq 0, \end{array}
The primal and dual feasible spaces would be: 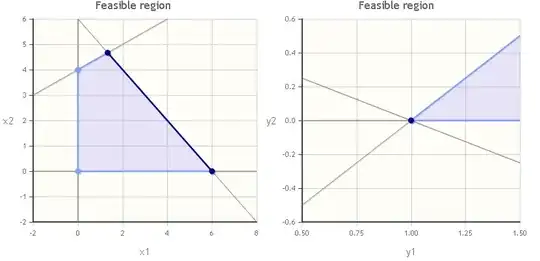The primal problem has four vertices, but the dual has one and obviously degenerated.

I think, as other members pointed out too, one of the best way to find the vertices in the primal or dual would be by using Simplex algorithm and information in its tableaus.

Answer 2

If you by standard form mean the primal-dual pair $$ \begin{array}{l} \text{minimize} & c^T x,\\ \text{subject to}& Ax=b,\\ &x\geq 0, \end{array} \quad \begin{array}{l} \text{maximize} & b^T y,\\ \text{subject to}& A^T y + s = c,\\ &s\geq 0, \end{array} $$

then

• primal feasible set is nonempty $\Leftrightarrow$ primal feasible set has an extreme point,
• dual feasible set is nonempty $\Leftrightarrow$ dual feasible set has an extreme point,

and you can find these extreme points using primal simplex phase I (resp. dual simplex phase I).

The stated assumption that the primal LP is feasible and has extreme points, notably does not imply that the dual is feasible and so does not imply that the dual has extreme points. Any primal problem with unbounded optimal value (objective can be improved indefinitely) will show you this.

Note further that standard forms allowing free variables in the primal and/or dual problem does not possess this property. Specifically, adding a free variable to any primal instance without any additional constraints will turn all of its feasible points non-extreme, while not affecting the extreme point property in the dual.

Answer 3

This turns out to be a bit tricky, in part because the geometry of a LP (feasible region, optimal points) can map to multiple algebraic formulations.

Consider the following admittedly goofy-looking LP: \begin{align*} \min5x-2y\\ \textrm{s.t. }x-y & =1\\ x-y & =1\\ x,y & \ge0 \end{align*} where the lone constraint is intentionally duplicated. It has one extreme point, namely $(1,0),$ which is also the optimal solution.

The dual problem is \begin{align*} \max\lambda+\mu\\ \textrm{s.t. }\lambda+\mu & \le5\\ -\lambda-\mu & \le-2\\ \lambda,\mu & \textrm{ free}. \end{align*} The feasible region of the dual is the infinite band $2 \le \lambda + \mu \le 5,$ which contains no extreme points. If we remove the redundant constraint in the primal, the dual has a single variable $\lambda$ with feasible region $2 \le \lambda \le 5,$ which clearly has extreme points.