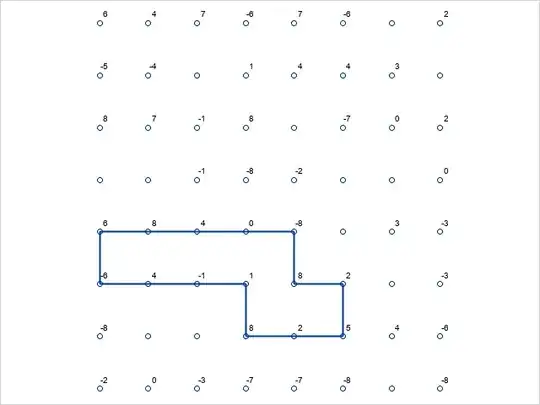
Given a n×m grid with numbered cells and forbidden cells, the objective of the Rogo puzzle is to find a loop of fixed length through the grid such that the sum of the numbers in the cells on the loop is maximized. Some cells should be avoided. ROGO Puzzle
How to add this constraint as a set of mixed integer linear constraints?
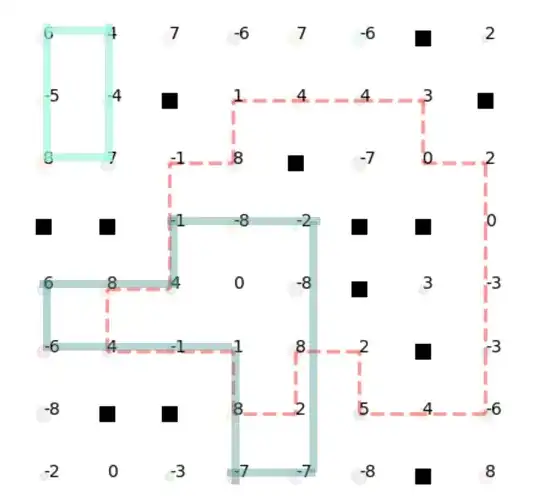
We need to make sure no Banned cell (black square) is trapped in the closed route?
The following red route is optimal (maxizes the total values but it contains black squares.
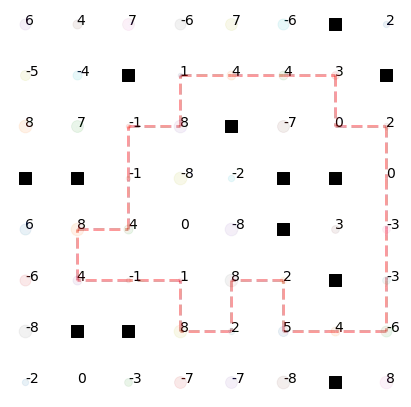
Two feasible routes are shown as follows: