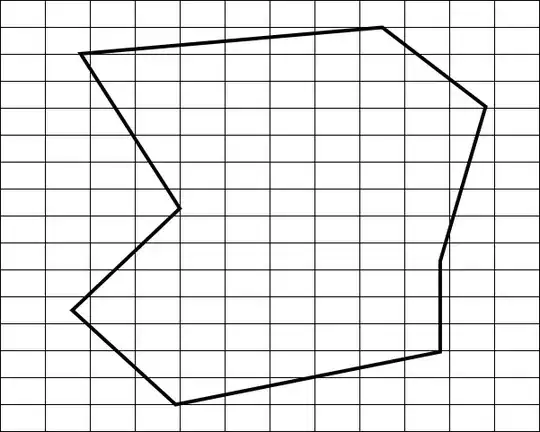
I have the following problem which seems related to the packing problem. I have a grid of same size rectangles and a polygon on which this grid of rectangles needs to be placed such that the number of rectangles completely withing the polygon boundaries are maximized. I have added a picture which shows a polygon and a grid of rectangles to illustrate the problem. The polygon can also contain holes.
My current algorithmic approach is just to orientate the grid the same way as the longest edge in the polygon. The algorithm needs to be fast, the solution does not need to be optimal. Are there any similiar problems in literature I can read up on?
Also the grid can be rotated and translated arbitrarily.