6

We optimize large-scale optimization problems with tens of thousands of variables and constraints with Cvxpy + Commercial solvers (e.g. Gurobi, Mosek).

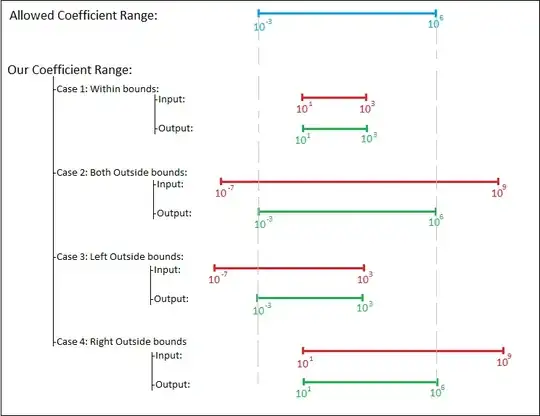
The coefficient range easily exceeds the recommended bounds of [1e-3, 1e+6], which eventually leads to numerical instability. This is the pain-point.

As a resolution, we wanted to scale the coefficients of the optimization problem (specifically linear constraints: A@x <= b, where $A\in\Bbb R^2$, $b\in\Bbb R$), such that all scaled coefficients lie within [1e-3, 1e+6].

E.g.

  • Raw constraint: $10^5x_1 + 10^7 x_2 \le 10^9$
  • Now, using Scaling factor = $10^5$ and Dividing both sides by scaling factor
  • Scaled constraint: $x_1 + 10^2 x_2 \le 10^4$

In general, the Scaling factor should behave like:

enter image description here

So, we were curious on:

  1. What should be the (row-wise) scaling factor vector $α = [α_1, α_2, ...]$ such that $(A/α) @ x \le (b/α)$ is a scaled constraint (i.e. all coefficient within [1e-3, 1e+6]) ?

Note: Here $α_i$ is scaling factor for the i-th row, i.e. $A_i @ x \le b_i$)

ə̷̶̸͇̘̜́̍͗̂̄︣͟
  • 5,412
  • 5
  • 22
  • 55
pqrz
  • 470
  • 2
  • 7
  • 1
    My recommendation is starting by choosing decent units for variables and constraints. That should result in a reasonable well scaled model. See also https://twitter.com/e_d_andersen/status/1245345927411503104 – ErlingMOSEK Mar 28 '22 at 05:18
  • 2
    Btw you can see an interior-point method as a method for finding a scaling that makes the problem trivial solvable. Therefore, scaling is as hard as solving the problem in general. – ErlingMOSEK Mar 28 '22 at 07:07
  • Thanks a lot Erling, Mathematically speaking, would this be almost equivalent to dividing by row minimum $A_i.min()$ – pqrz Mar 28 '22 at 09:39

1 Answers1

4

You cannot necessarily achieve this by scaling only rows. Consider case 2 in your chart. The ratio of largest to smallest (nonzero) coefficient magnitude is $10^9/10^{-7}=10^{16}.$ The target range ("output") would have a ratio of $10^6/10^{-3}=10^9.$ The problem is that scaling the row by a constant factor does not change the ratio.

So you will need to scale both rows and columns ... and even with that, I'm not sure you can guarantee hitting all your targets.

prubin
  • 39,078
  • 3
  • 37
  • 104
  • Thanks for your comments! Very frankly speaking, this is slightly strange, that even scaling is still a unsolvable mathematical problem. – pqrz Mar 27 '22 at 15:14
  • I totally agree with the Case 2 example you mentioned, it is reasonable. If not all (i.e. ignoring case 2) - what can be the best that we can do (i.e. case 1, case 3, case 4)? – pqrz Mar 27 '22 at 15:16
  • 3
    Scaling LP and MIP models is an ongoing research topic. See, for instance, http://www.optimization-online.org/DB_HTML/2020/12/8166.html. I think most solvers try to do some scaling automatically, and may have parameters that let you decide how (or how aggressively) to try to scale the problem. – prubin Mar 27 '22 at 16:21
  • 1
    I don't know that anyone does it, but in theory you could solve an integer programming with more variables and constraints (but likely sparser) than your original problem to find the optimal scaling. It sounds a bit dopey, but conceivably it might solve in "reasonable" time, and if your original model cannot be solved due to numerical problems it might be worth the effort. – prubin Mar 27 '22 at 16:24
  • Sorry, typo in my last comment: you would be solving an LP, not an IP, for the scale factors. – prubin Mar 27 '22 at 21:32