Help modeling grid placement problem

Question

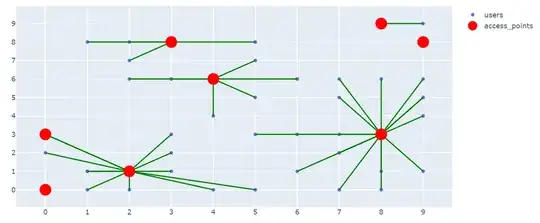
I'm trying to model a grid placement problem to exercise in OR.

The problem is defined as:

a grid of some dimension (let's say 500x500)
N users that need connection. Every user has:
- a defined position on the grid
- a speed value
- a latency value
M wifi access points to place on the grid. Every access point has:
- a range
- a speed value

Objective is to maximize: $$\sum_{n \in N} user\_score(n)$$ given $$user\_score(n) = \max_{m \in M} score(n, m)$$ $$score(n, m) = \begin{cases} speed(n) * speed(m) - latency(n) * distance(n,m) & distance(n,m) <= range(m)\\ 0 & distance(n,m) > range(m) \end{cases}$$ $$distance(n,m) = abs(n_x - m_x) + abs(n_y - m_y) \space\space\text{(manhattan distance)}$$

Additional rules:

two access points can't share the same location on the grid
an access point and a user can share the same location
if no access point is in range, user score is 0

I tried modeling it as follows, using or-tools:

model = cp.CpModel()
all_x = []
all_y = []
all_k = []
for a in access_points:
    x = model.NewIntVar(0, grid_w - 1, f'x_{a.id}')
    y = model.NewIntVar(0, grid_h - 1, f'y_{a.id}')
    k = model.NewIntVar(0, (grid_w - 1) * 1000 + grid_h, f'k_{a.id}')
model.Add(k == x * 1000 + y)

all_x.append(x)
all_y.append(y)
all_k.append(k)


model.AddAllDifferent(all_k)
scores = []
for b in users
u_score = model.NewIntVar(0, cp.INT32_MAX, f'u_score_{b.id}')
all_u_scores = []

for ia, a in enumerate(access_points):

    abs_x = model.NewIntVar(0, grid_w, f'abs_x_{b.id}_{a.id}')
    abs_y = model.NewIntVar(0, grid_h, f'abs_y_{b.id}_{a.id}')

    model.AddAbsEquality(abs_x, all_x[ia] - b.x)
    model.AddAbsEquality(abs_y, all_y[ia] - b.y)

    in_range = model.NewBoolVar(f'in_range_{b.id}_{a.id}')
    model.Add(abs_x + abs_y &lt;= a.range).OnlyEnforceIf(in_range)
    model.Add(abs_x + abs_y &gt; a.range).OnlyEnforceIf(in_range.Not())

    score = model.NewIntVar(0, cp.INT32_MAX, f'score_{b.id}_{a.id}')
    model.Add(score == 0).OnlyEnforceIf(in_range.Not())
    model.Add(score == a.speed * b.speed - b.latency * (abs_x + abs_y)).OnlyEnforceIf(in_range)

    all_b_scores.append(score)

model.AddMaxEquality(b_score, all_b_scores)

scores.append(b_score)


model.Maximize(sum(scores))

This works well with a small grid with a few users/access points, but scales bad on bigger problem instances.

Is the model good? Any better way to model the problem?

This looks like a facility location problem. – Kuifje Mar 03 '22 at 14:26 — Kuifje, Mar 03 '22 at 14:26

Kuifje · Answer 1 · 2022-03-05T16:40:42.380

7

Let $x_{ij}^p$ be a binary variable that indicates if user $i\in I$ is assigned to access point $j \in J = \{1,...,M\}$ located in position $p\in P$, and let $z_{j}^p$ be a binary variable that indicates if access point $j\in J$ is assigned to position $p\in P$.

For every tuple $(i,j,p) \in I \times J \times P$, a score $c_{ij}^p$ is computed according OP's rules: $$ c_{ij}^p = \begin{cases} 0 & \mbox{ if } d_{ip} > \mbox{range}(j) \\ \mbox{speed}(i)\cdot\mbox{speed}(j)- \mbox{latency}(i)\cdot d_{ip}& \mbox{ otherwise } \end{cases} $$

You want to maximize the total score: $$ \max \; \sum_i\sum_j\sum_p c_{ij}^p x_{ij}^p $$ subject to

assign users to access points: $$ \sum_j\sum_p x_{ij}^p = 1 \quad \forall i \in I $$
each access point has a unique position: $$ \sum_p z_{j}^p = 1 \quad \forall j \in J $$
each position has at most one access point: $$ \sum_j z_{j}^p \le 1 \quad \forall p \in P $$
consistency between $x_{ij}^p$ and $z_{j}^p$: $$ x_{ij}^p \le z_{j}^p \quad \forall i \in I, \forall j \in J, \forall p \in P $$

You might want to consider maximizing the minimum score.

My simulations with some random data (possibly poorly randomized and scaled) yield the following output:

edited Mar 05 '22 at 16:40

answered Mar 03 '22 at 17:43

Kuifje

13,324
1
23
56

Thanks for the reply. If i understood correctly, I should have an $y_j$ variable for each grid position for each access point. Additionally, each user should be linked to each of these access point positions by $X_{ij}$ This means that I woud have, given an $N \times M$ grid with $I$ users and $J$ access points, $N \times M \times I \times J$ variables $x_{ij}$.
Is that correct?
– rsella Mar 03 '22 at 21:42
Not exactly. If you have an $N\times M$ grid, then $J=N \times M$, so you would have $I\times N \times M$ $x$ variables. That said, you may not have to define them all. You could define only the ones for which the score is positive, and see if it is feasible. – Kuifje Mar 04 '22 at 08:46
I'm missing something. Every position in the grid can contain any of the access points, that have different ranges. So $c_{ij}$ can't be defined if $j \in J$ with $J = N \times M$, because $range(j)$ is not known as it depends on the range of the access point placed at $j$ – rsella Mar 04 '22 at 20:00
OK, i see. I have edited accordingly. – Kuifje Mar 05 '22 at 00:45

Help modeling grid placement problem

1 Answers1