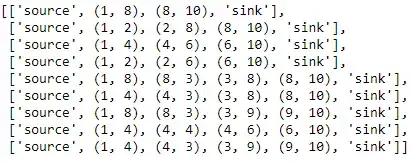How to compute all paths between two given nodes in a network?

Question

In this post, Erwin Kalvelagen describes a method to compute all paths between two nodes in a given network, such that:

• no arc is used more than once
• a given path does not contain more than $M$ arcs

Note that nodes can be revisited, and this is part of the difficulty. His approach is well described and involves using the line graph, MTZ constraints, and a solution pool approach.

Are there other ways to tackle this problem (brute force excluded) ?

---

This problem was initially posted on stackoverflow, but the question seems to have been removed. I believe it is of interest to the OR community, as the problem is more complicated than it looks.

@ErwinKalvelagen, feel free to post bits of your answer here, will be happy to upvote it given that it originated this post.

Answer 1

I would solve this using the following approach:

1. Compute the shortest path with a MIP, with an additional constraint to limit the number of arcs in the path.
2. If a path is found, store it, add a no good cut to exclude this path in the next iterations, and go to step 1. If no path is found, you are done.

The tricky part is to use the right no good cut for a given path $P$. It needs to exclude the path that has been found, except if it includes other edges of the network without forming a subtour (Erwin Kalvelagen used MTZ constraints to forbid subtours).

For example, if $P=1-8-10$, path $Q=1-8-3-8-10$ is a candidate (if $M=4$). On the other hand, a solution with edges $(1,8),(8,10),(4,4)$ (that is, $P$ with an isolated self-loop) must be forbidden. In other words, the no good cuts must ensure some sort of contiguity if edges from $P$ are used again.

This can be done as follows: $$ \sum_{(i,j)\in P}(1-x_{ij}) + \sum_{(i,j)\not \in P, i\in P \mbox{ or } j \in P}x_{ij} \ge 1 $$ This means that

1. Either one of the edges of $P$ must take value $0$ (and so the path will be different from $P$) or
2. Either one of the edges of the network not in $P$, but linked to $P$ must be used (in which case $P$ will have extra edges, without subtours).

My simulations with this approach match Erwin's results. Downside: you have to solve a series of MIPs, possibly many. Upside: no graph transformation (line graph), and no MTZ constraints.

---

EDIT

This strategy has the following flaw for graphs that have multiple subtours originating at a same node. For example consider paths $P=1-u-a-u-b-u-10$ and $Q=1-u-b-u-a-u-10$: they have the exact same edge set, but the order of the nodes differ. Once path $P$ is found, path $Q$ will become infeasible with respect to the no good cut associated with $P$. In other words the no good cuts are too strong.

There are at least two ways to fix this:

1. Once a path is generated, check if this situation occurs and deduce all possible paths. This is doable but a bit tedious.
2. Use the line graph. This is handy because with the line graph, no loops are possible. So the MIP can be solved on the line graph, with the following no good cuts for a given path $P$: \begin{align*} \sum_{((u,v),(x,y))\in P}(1-x_{u,v,x,y}) &\ge 1 \tag{1} \\ \sum_{((u,v),(x,y))\not \in P}x_{u,v,x,y} &\ge 2 \tag{2} \end{align*}

Constraints $(1)$ impose that at least one edge from $P$ must be removed and constraints $(2)$ impose that at least $2$ new edges must be selected.

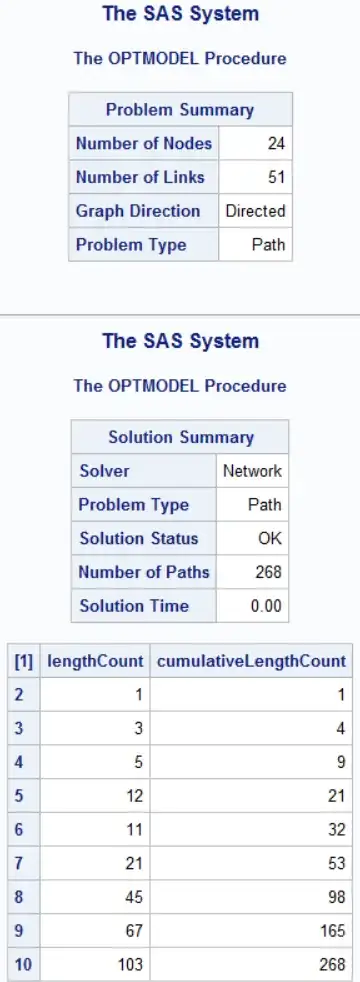
With these new cuts, I get the following results, which match with the other approaches suggested in the other answers:

M	2	3	4	5	6	7	8	9	10
paths	1	4	9	21	32	53	98	165	268

Answer 2

Yet another possibility suggested by @Sune, using $k$-shortest path algorithms :

The python module NetworkX provides an implementation of Yens's algorithm. Since the algorithm computes loopless paths, using the line graph like Erwin is necessary. Once the transformation is done, it is a one liner:

# create line graph
H = nx.line_graph(G)
new_edges = []
# add source and sink nodes
for (u,v) in H.nodes():
    if u==1:
        new_edges.append(("source",(u,v)))
    if v==10:
        new_edges.append(((u,v),"sink"))
H.add_edges_from(new_edges)
9 shortest paths
list(islice(nx.shortest_simple_paths(H, source="source", target="sink"), 9))

Erwin's graph is solved in less than $0.1$ ms, and the output is, as expected:

Answer 3

I tried an alternative (possibly over-engineered) MIP formulation, using Miller-Tucker-Zemlin variables. $A$ is the set of arcs in the graph, $s$ is the source node for all paths, and $t$ is the sink node for all paths. $M$ is the maximum path length. The variables are as follows.

• $u_{a}\in\left\{ 0,1\right\} $ is 1 if and only if arc $a$ is used on the path.
• $f_{a}\in\left\{ 0,1\right\} $ is 1 if and only if arc $a$ is the first arc on the path.
• $\ell_{a}\in\left\{ 0,1\right\} $ is 1 if and only if arc $a$ is the last arc on the path.
• $y_{ab}\in\left\{ 0,1\right\} $ is 1 if and only if arc $b$ immediately follows arc $a$ on the path.
• $z_{a}\in\left[0,M\right]$ will be the number of arcs preceding arc $a$ on the path (0 if $a$ is not on the path).

We can fix the values of many of the variables up front.

• $f_{a}=0$ if node $s$ is not the tail of arc $a.$
• $\ell_{a}=0$ if node $t$ is not the head of arc $a.$
• $y_{ab}=0$ if the head of arc $a$ is not the tail of arc $b.$

The constraints are as follows.

• There must be one first arc and one last arc. $$\sum_{a\in A}f_{a}=1.$$ $$\sum_{a\in A}\ell_{a}=1.$$
• At most $M$ arcs can be used. $$\sum_{a\in A}u_{a}\le M.$$
• An arc is used if and only if it is either the first arc or follows another arc on the path. $$f_{a}+\sum_{b\in A}y_{ba}=u_{a}\quad\forall a\in A.$$
• The last arc must be a used arc. $$\ell_{a}\le u_{a}\quad\forall a\in A.$$
• The sequence value of an unused arc is 0. $$z_{a}\le Mu_{a}\quad\forall a\in A.$$
• No arc can follow the last arc. $$\ell_{a}+\sum_{b\in A}y_{ab}\le1\quad\forall a\in A.$$
• If an arc is used, either it is the last arc or another arc follows it. $$\ell_{a}+\sum_{b\in A}y_{ab}=u_{a}\quad\forall a\in A.$$
• If an arc $b$ follows arc $a$, the sequence number of arc $b$ must be one higher than the sequence number of arc $a$ (MTZ). $$z_{a}-z_{b}+\left(M+1\right)y_{ab}\le M\quad\forall a,b\in A,a\neq b.$$

I omitted an objective function, which is equivalent to making the objective function minimizing a constant (0).

Rather than solving repeatedly with no-good constraints added after each new solution, I used the "populate" function in CPLEX with suitable parameters to get all feasible solutions in one gulp. That worked for $M=3$ and $M=4$, but on Erwin's graph with $M=10$ brute force found 268 paths and the populate function (with the highest intensity setting and a large pool capacity setting) found only 33.

Answer 4

Here's an approach that uses the network solver in SAS (disclaimer: I work at SAS) to enumerate all elementary paths in the line graph up to a maximum length:

data indata;
   input i j @@;
   from = compress(i||'');
   to   = compress(j||'');
   datalines;
1 2  1 4  1 8
2 6  2 8
3 3  3 8  3 9
4 3  4 4  4 6  4 7
5 9
6 5  6 10
7 1  7 5
8 3  8 10
9 1  9 7  9 10
;
proc optmodel;
   /* read original data */
   set <str,str> LINKS_ORIG;
   read data indata into LINKS_ORIG=[from to];
   LINKS_ORIG = LINKS_ORIG union {<'source','1'>,<'10','sink'>};
/* construct line graph */
   set SOURCE = {'source_1'};
   set SINK   = {'10_sink'};
   set LINKS = setof {<i,j> in LINKS_ORIG, <(j),k> in LINKS_ORIG diff {<i,j>}} <i||''||j, j||''||k>;
/* call network solver /
   set <str,str,num,num,str,str> PATHSLINKS; / <source,sink,id,order,from,to> */
   solve with network / path=(source=SOURCE sink=SINK maxlength=11) direction=directed links=(include=LINKS) out=(pathslinks=PATHSLINKS);
/* count path lengths */
   set PATHS = 1..OROPTMODEL_NUM['NUM_PATHS'];
   num length {PATHS} init -1;
   for {<s,t,p,o,from,to> in PATHSLINKS} length[p] = length[p] + 1;
   num len;
   set LENGTHS init {};
   num lengthCount {LENGTHS} init 0;
   for {p in PATHS} do;
      len = length[p];
      LENGTHS = LENGTHS union {len};
      lengthCount[len] = lengthCount[len] + 1;

   end;
   num cumulativeLengthCount {l in LENGTHS} = lengthCount[l] + (if l-1 in LENGTHS then cumulativeLengthCount[l-1]);
   print lengthCount cumulativeLengthCount;
quit;

You can also find the $9$ shortest paths as in @Kuifje's answer by changing the SOLVE statement as follows:

   solve with network / shortpath=(source=SOURCE sink=SINK maxPathsPerPair=9) direction=directed links=(include=LINKS) out=(pathslinks=PATHSLINKS);

Answer 5

I am trying to use the critical path method with a bit of modification to find all of the paths on the directed graph. Also, this is my first attempt and I am pretty sure that it can be better with some of the trials and errors. Indeed, I should work on the capture of the second limitation (a given path does not contain more than M arcs). What I do comes in the following comments of the original question.

The CPM is the fundamental algorithm to find the completion time of the project schedule problems on many of the commercial software. I am using a simple example to make a comparison on what @Kuifje purposed.

In the following network there are three paths:

By calculation of the either forward and backward passes in the CPM, the following results are figured out:

task id, task name, active
10,       A,          True
20,       B,          True
25,       C,          True
30,       D,          True
40,       E,          True

In the above table, the numbers $10, 20, 25, 30, 40$ are corresponding to the nodes $0, 1, 2, 3, 4$ respectively and it means that all of the three paths are active. The achieved result by @Kuifje formulation is also equal to three.