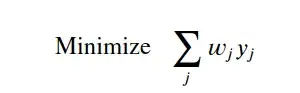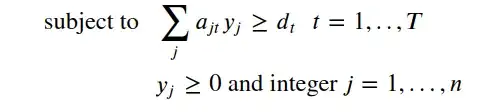Python Pulp - LpMinimize Not Returning Expected Output - Scheduling Problem

Question

I'm working on my first pulp model and something isn't going quite right. It looks like it's close, but for some reason it is not respecting one of my constraints...

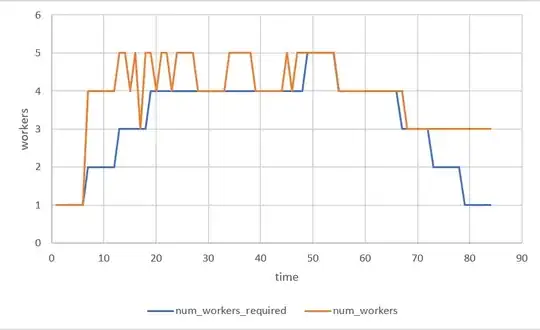
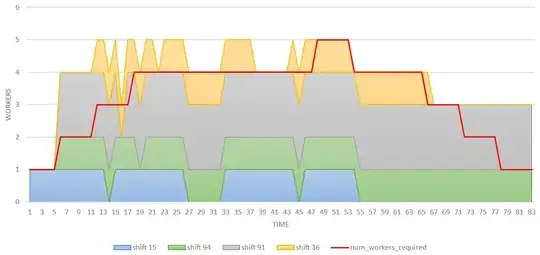
It's a scheduling problem and I am trying to minimize the number of labor hours used whilst meeting the workforce requirements for each time window. The model returns an "optimal" result, but the staffing figures are far short of the workforce requirements for each window.

There are 120 potential shifts to choose from ("n"), and 84 time windows (t). Each time window has its own workforce requirement (number of staff, "d"). Not all shifts will be filled.

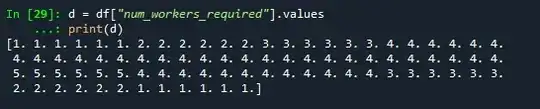
"d" is the number of workers required in each of the 84 time windows, it is as follows:

I want to minimize the number of labor hours required in total ("w") whilst meeting the workforce requirements for each time window. "w" looks like this, in hours per shift - one entry for each of the 120 potential shifts:

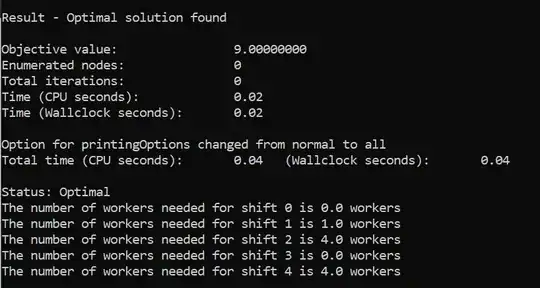
The final solution does not satisfy the workforce requirements for the various time windows, it's substantially short. Only 5 shifts are filled in total:

Status: Optimal
The number of workers needed for shift 0 is 1 workers
The number of workers needed for shift 90 is 2 workers
The number of workers needed for shift 91 is 1 workers
The number of workers needed for shift 92 is 1 workers

For reference, just to show that the needed amount of labor isn't in the solution, these are the full schedules for each of the 120 shifts (asterisks on the shifts that the solver filled (1, 89 (2 employees), 90, and 91):

Shift_Num	Start_Shift	First_Break_Start	First_Break_End	Lunch_Start	Lunch_End	Second_Break_Start	Second_Break_End	End_Shift
***1	5:00:00 AM	6:40:00 AM	6:50:00 AM	9:00:00 AM	10:00:00 AM	11:40:00 AM	11:50:00 AM	2:00:00 PM
2	5:00:00 AM	6:50:00 AM	7:00:00 AM	9:00:00 AM	10:00:00 AM	11:50:00 AM	12:00:00 PM	2:00:00 PM
3	5:00:00 AM	7:00:00 AM	7:10:00 AM	9:00:00 AM	10:00:00 AM	12:00:00 PM	12:10:00 PM	2:00:00 PM
4	5:00:00 AM	7:10:00 AM	7:20:00 AM	9:00:00 AM	10:00:00 AM	12:10:00 PM	12:20:00 PM	2:00:00 PM
5	5:00:00 AM	7:20:00 AM	7:30:00 AM	9:00:00 AM	10:00:00 AM	12:20:00 PM	12:30:00 PM	2:00:00 PM
6	5:00:00 AM	6:40:00 AM	6:50:00 AM	9:15:00 AM	10:15:00 AM	11:55:00 AM	12:05:00 PM	2:00:00 PM
7	5:00:00 AM	6:50:00 AM	7:00:00 AM	9:15:00 AM	10:15:00 AM	12:05:00 PM	12:15:00 PM	2:00:00 PM
8	5:00:00 AM	7:00:00 AM	7:10:00 AM	9:15:00 AM	10:15:00 AM	12:15:00 PM	12:25:00 PM	2:00:00 PM
9	5:00:00 AM	7:10:00 AM	7:20:00 AM	9:15:00 AM	10:15:00 AM	12:25:00 PM	12:35:00 PM	2:00:00 PM
10	5:00:00 AM	7:20:00 AM	7:30:00 AM	9:15:00 AM	10:15:00 AM	12:35:00 PM	12:45:00 PM	2:00:00 PM
11	5:00:00 AM	6:40:00 AM	6:50:00 AM	9:30:00 AM	10:30:00 AM	12:00:00 PM	12:10:00 PM	2:00:00 PM
12	5:00:00 AM	6:50:00 AM	7:00:00 AM	9:30:00 AM	10:30:00 AM	12:10:00 PM	12:20:00 PM	2:00:00 PM
13	5:00:00 AM	7:00:00 AM	7:10:00 AM	9:30:00 AM	10:30:00 AM	12:20:00 PM	12:30:00 PM	2:00:00 PM
14	5:00:00 AM	7:10:00 AM	7:20:00 AM	9:30:00 AM	10:30:00 AM	12:30:00 PM	12:40:00 PM	2:00:00 PM
15	5:00:00 AM	7:20:00 AM	7:30:00 AM	9:30:00 AM	10:30:00 AM	12:30:00 PM	12:40:00 PM	2:00:00 PM
16	6:00:00 AM	7:40:00 AM	7:50:00 AM	10:00:00 AM	11:00:00 AM	12:40:00 PM	12:50:00 PM	3:00:00 PM
17	6:00:00 AM	7:50:00 AM	8:00:00 AM	10:00:00 AM	11:00:00 AM	12:50:00 PM	1:00:00 PM	3:00:00 PM
18	6:00:00 AM	8:00:00 AM	8:10:00 AM	10:00:00 AM	11:00:00 AM	1:00:00 PM	1:10:00 PM	3:00:00 PM
19	6:00:00 AM	8:10:00 AM	8:20:00 AM	10:00:00 AM	11:00:00 AM	1:10:00 PM	1:20:00 PM	3:00:00 PM
20	6:00:00 AM	8:20:00 AM	8:30:00 AM	10:00:00 AM	11:00:00 AM	1:20:00 PM	1:30:00 PM	3:00:00 PM
21	6:00:00 AM	7:40:00 AM	7:50:00 AM	10:15:00 AM	11:15:00 AM	12:55:00 PM	1:05:00 PM	3:00:00 PM
22	6:00:00 AM	7:50:00 AM	8:00:00 AM	10:15:00 AM	11:15:00 AM	1:05:00 PM	1:15:00 PM	3:00:00 PM
23	6:00:00 AM	8:00:00 AM	8:10:00 AM	10:15:00 AM	11:15:00 AM	1:15:00 PM	1:25:00 PM	3:00:00 PM
24	6:00:00 AM	8:10:00 AM	8:20:00 AM	10:15:00 AM	11:15:00 AM	1:25:00 PM	1:35:00 PM	3:00:00 PM
25	6:00:00 AM	8:20:00 AM	8:30:00 AM	10:15:00 AM	11:15:00 AM	1:35:00 PM	1:45:00 PM	3:00:00 PM
26	6:00:00 AM	7:40:00 AM	7:50:00 AM	10:30:00 AM	11:30:00 AM	1:00:00 PM	1:10:00 PM	3:00:00 PM
27	6:00:00 AM	7:50:00 AM	8:00:00 AM	10:30:00 AM	11:30:00 AM	1:10:00 PM	1:20:00 PM	3:00:00 PM
28	6:00:00 AM	8:00:00 AM	8:10:00 AM	10:30:00 AM	11:30:00 AM	1:20:00 PM	1:30:00 PM	3:00:00 PM
29	6:00:00 AM	8:10:00 AM	8:20:00 AM	10:30:00 AM	11:30:00 AM	1:30:00 PM	1:40:00 PM	3:00:00 PM
30	6:00:00 AM	8:20:00 AM	8:30:00 AM	10:30:00 AM	11:30:00 AM	1:30:00 PM	1:40:00 PM	3:00:00 PM
31	7:00:00 AM	8:40:00 AM	8:50:00 AM	11:00:00 AM	12:00:00 PM	1:40:00 PM	1:50:00 PM	4:00:00 PM
32	7:00:00 AM	8:50:00 AM	9:00:00 AM	11:00:00 AM	12:00:00 PM	1:50:00 PM	2:00:00 PM	4:00:00 PM
33	7:00:00 AM	9:00:00 AM	9:10:00 AM	11:00:00 AM	12:00:00 PM	2:00:00 PM	2:10:00 PM	4:00:00 PM
34	7:00:00 AM	9:10:00 AM	9:20:00 AM	11:00:00 AM	12:00:00 PM	2:10:00 PM	2:20:00 PM	4:00:00 PM
35	7:00:00 AM	9:20:00 AM	9:30:00 AM	11:00:00 AM	12:00:00 PM	2:20:00 PM	2:30:00 PM	4:00:00 PM
36	7:00:00 AM	8:40:00 AM	8:50:00 AM	11:15:00 AM	12:15:00 PM	1:55:00 PM	2:05:00 PM	4:00:00 PM
37	7:00:00 AM	8:50:00 AM	9:00:00 AM	11:15:00 AM	12:15:00 PM	2:05:00 PM	2:15:00 PM	4:00:00 PM
38	7:00:00 AM	9:00:00 AM	9:10:00 AM	11:15:00 AM	12:15:00 PM	2:15:00 PM	2:25:00 PM	4:00:00 PM
39	7:00:00 AM	9:10:00 AM	9:20:00 AM	11:15:00 AM	12:15:00 PM	2:25:00 PM	2:35:00 PM	4:00:00 PM
40	7:00:00 AM	9:20:00 AM	9:30:00 AM	11:15:00 AM	12:15:00 PM	2:35:00 PM	2:45:00 PM	4:00:00 PM
41	7:00:00 AM	8:40:00 AM	8:50:00 AM	11:30:00 AM	12:30:00 PM	2:00:00 PM	2:10:00 PM	4:00:00 PM
42	7:00:00 AM	8:50:00 AM	9:00:00 AM	11:30:00 AM	12:30:00 PM	2:10:00 PM	2:20:00 PM	4:00:00 PM
43	7:00:00 AM	9:00:00 AM	9:10:00 AM	11:30:00 AM	12:30:00 PM	2:20:00 PM	2:30:00 PM	4:00:00 PM
44	7:00:00 AM	9:10:00 AM	9:20:00 AM	11:30:00 AM	12:30:00 PM	2:30:00 PM	2:40:00 PM	4:00:00 PM
45	7:00:00 AM	9:20:00 AM	9:30:00 AM	11:30:00 AM	12:30:00 PM	2:30:00 PM	2:40:00 PM	4:00:00 PM
46	8:00:00 AM	9:40:00 AM	9:50:00 AM	12:00:00 PM	1:00:00 PM	2:40:00 PM	2:50:00 PM	5:00:00 PM
47	8:00:00 AM	9:50:00 AM	10:00:00 AM	12:00:00 PM	1:00:00 PM	2:50:00 PM	3:00:00 PM	5:00:00 PM
48	8:00:00 AM	10:00:00 AM	10:10:00 AM	12:00:00 PM	1:00:00 PM	3:00:00 PM	3:10:00 PM	5:00:00 PM
49	8:00:00 AM	10:10:00 AM	10:20:00 AM	12:00:00 PM	1:00:00 PM	3:10:00 PM	3:20:00 PM	5:00:00 PM
50	8:00:00 AM	10:20:00 AM	10:30:00 AM	12:00:00 PM	1:00:00 PM	3:20:00 PM	3:30:00 PM	5:00:00 PM
51	8:00:00 AM	9:40:00 AM	9:50:00 AM	12:15:00 PM	1:15:00 PM	2:55:00 PM	3:05:00 PM	5:00:00 PM
52	8:00:00 AM	9:50:00 AM	10:00:00 AM	12:15:00 PM	1:15:00 PM	3:05:00 PM	3:15:00 PM	5:00:00 PM
53	8:00:00 AM	10:00:00 AM	10:10:00 AM	12:15:00 PM	1:15:00 PM	3:15:00 PM	3:25:00 PM	5:00:00 PM
54	8:00:00 AM	10:10:00 AM	10:20:00 AM	12:15:00 PM	1:15:00 PM	3:25:00 PM	3:35:00 PM	5:00:00 PM
55	8:00:00 AM	10:20:00 AM	10:30:00 AM	12:15:00 PM	1:15:00 PM	3:35:00 PM	3:45:00 PM	5:00:00 PM
56	8:00:00 AM	9:40:00 AM	9:50:00 AM	12:30:00 PM	1:30:00 PM	3:00:00 PM	3:10:00 PM	5:00:00 PM
57	8:00:00 AM	9:50:00 AM	10:00:00 AM	12:30:00 PM	1:30:00 PM	3:10:00 PM	3:20:00 PM	5:00:00 PM
58	8:00:00 AM	10:00:00 AM	10:10:00 AM	12:30:00 PM	1:30:00 PM	3:20:00 PM	3:30:00 PM	5:00:00 PM
59	8:00:00 AM	10:10:00 AM	10:20:00 AM	12:30:00 PM	1:30:00 PM	3:30:00 PM	3:40:00 PM	5:00:00 PM
60	8:00:00 AM	10:20:00 AM	10:30:00 AM	12:30:00 PM	1:30:00 PM	3:30:00 PM	3:40:00 PM	5:00:00 PM
61	9:00:00 AM	10:40:00 AM	10:50:00 AM	1:00:00 PM	2:00:00 PM	3:40:00 PM	3:50:00 PM	6:00:00 PM
62	9:00:00 AM	10:50:00 AM	11:00:00 AM	1:00:00 PM	2:00:00 PM	3:50:00 PM	4:00:00 PM	6:00:00 PM
63	9:00:00 AM	11:00:00 AM	11:10:00 AM	1:00:00 PM	2:00:00 PM	4:00:00 PM	4:10:00 PM	6:00:00 PM
64	9:00:00 AM	11:10:00 AM	11:20:00 AM	1:00:00 PM	2:00:00 PM	4:10:00 PM	4:20:00 PM	6:00:00 PM
65	9:00:00 AM	11:20:00 AM	11:30:00 AM	1:00:00 PM	2:00:00 PM	4:20:00 PM	4:30:00 PM	6:00:00 PM
66	9:00:00 AM	10:40:00 AM	10:50:00 AM	1:15:00 PM	2:15:00 PM	3:55:00 PM	4:05:00 PM	6:00:00 PM
67	9:00:00 AM	10:50:00 AM	11:00:00 AM	1:15:00 PM	2:15:00 PM	4:05:00 PM	4:15:00 PM	6:00:00 PM
68	9:00:00 AM	11:00:00 AM	11:10:00 AM	1:15:00 PM	2:15:00 PM	4:15:00 PM	4:25:00 PM	6:00:00 PM
69	9:00:00 AM	11:10:00 AM	11:20:00 AM	1:15:00 PM	2:15:00 PM	4:25:00 PM	4:35:00 PM	6:00:00 PM
70	9:00:00 AM	11:20:00 AM	11:30:00 AM	1:15:00 PM	2:15:00 PM	4:35:00 PM	4:45:00 PM	6:00:00 PM
71	9:00:00 AM	10:40:00 AM	10:50:00 AM	1:30:00 PM	2:30:00 PM	4:00:00 PM	4:10:00 PM	6:00:00 PM
72	9:00:00 AM	10:50:00 AM	11:00:00 AM	1:30:00 PM	2:30:00 PM	4:10:00 PM	4:20:00 PM	6:00:00 PM
73	9:00:00 AM	11:00:00 AM	11:10:00 AM	1:30:00 PM	2:30:00 PM	4:20:00 PM	4:30:00 PM	6:00:00 PM
74	9:00:00 AM	11:10:00 AM	11:20:00 AM	1:30:00 PM	2:30:00 PM	4:30:00 PM	4:40:00 PM	6:00:00 PM
75	9:00:00 AM	11:20:00 AM	11:30:00 AM	1:30:00 PM	2:30:00 PM	4:30:00 PM	4:40:00 PM	6:00:00 PM
76	10:00:00 AM	11:40:00 AM	11:50:00 AM	2:00:00 PM	3:00:00 PM	4:40:00 PM	4:50:00 PM	7:00:00 PM
77	10:00:00 AM	11:50:00 AM	12:00:00 PM	2:00:00 PM	3:00:00 PM	4:50:00 PM	5:00:00 PM	7:00:00 PM
78	10:00:00 AM	12:00:00 PM	12:10:00 PM	2:00:00 PM	3:00:00 PM	5:00:00 PM	5:10:00 PM	7:00:00 PM
79	10:00:00 AM	12:10:00 PM	12:20:00 PM	2:00:00 PM	3:00:00 PM	5:10:00 PM	5:20:00 PM	7:00:00 PM
80	10:00:00 AM	12:20:00 PM	12:30:00 PM	2:00:00 PM	3:00:00 PM	5:20:00 PM	5:30:00 PM	7:00:00 PM
81	10:00:00 AM	11:40:00 AM	11:50:00 AM	2:15:00 PM	3:15:00 PM	4:55:00 PM	5:05:00 PM	7:00:00 PM
82	10:00:00 AM	11:50:00 AM	12:00:00 PM	2:15:00 PM	3:15:00 PM	5:05:00 PM	5:15:00 PM	7:00:00 PM
83	10:00:00 AM	12:00:00 PM	12:10:00 PM	2:15:00 PM	3:15:00 PM	5:15:00 PM	5:25:00 PM	7:00:00 PM
84	10:00:00 AM	12:10:00 PM	12:20:00 PM	2:15:00 PM	3:15:00 PM	5:25:00 PM	5:35:00 PM	7:00:00 PM
85	10:00:00 AM	12:20:00 PM	12:30:00 PM	2:15:00 PM	3:15:00 PM	5:35:00 PM	5:45:00 PM	7:00:00 PM
86	10:00:00 AM	11:40:00 AM	11:50:00 AM	2:30:00 PM	3:30:00 PM	5:00:00 PM	5:10:00 PM	7:00:00 PM
87	10:00:00 AM	11:50:00 AM	12:00:00 PM	2:30:00 PM	3:30:00 PM	5:10:00 PM	5:20:00 PM	7:00:00 PM
88	10:00:00 AM	12:00:00 PM	12:10:00 PM	2:30:00 PM	3:30:00 PM	5:20:00 PM	5:30:00 PM	7:00:00 PM
***89	10:00:00 AM	12:10:00 PM	12:20:00 PM	2:30:00 PM	3:30:00 PM	5:30:00 PM	5:40:00 PM	7:00:00 PM
***90	10:00:00 AM	12:20:00 PM	12:30:00 PM	2:30:00 PM	3:30:00 PM	5:30:00 PM	5:40:00 PM	7:00:00 PM
***91	6:00:00 AM	7:40:00 AM	7:50:00 AM					10:00:00 AM
92	6:00:00 AM	7:50:00 AM	8:00:00 AM					10:00:00 AM
93	6:00:00 AM	8:00:00 AM	8:10:00 AM					10:00:00 AM
94	6:00:00 AM	8:10:00 AM	8:20:00 AM					10:00:00 AM
95	6:00:00 AM	8:20:00 AM	8:30:00 AM					10:00:00 AM
96	8:00:00 AM	10:10:00 AM	10:20:00 AM					1:00:00 PM
97	8:00:00 AM	10:20:00 AM	10:30:00 AM					1:00:00 PM
98	8:00:00 AM	10:30:00 AM	10:40:00 AM					1:00:00 PM
99	8:00:00 AM	10:40:00 AM	10:50:00 AM					1:00:00 PM
100	8:00:00 AM	10:50:00 AM	11:00:00 AM					1:00:00 PM
101	9:00:00 AM	11:10:00 AM	11:20:00 AM					2:00:00 PM
102	9:00:00 AM	11:20:00 AM	11:30:00 AM					2:00:00 PM
103	9:00:00 AM	11:30:00 AM	11:40:00 AM					2:00:00 PM
104	9:00:00 AM	11:40:00 AM	11:50:00 AM					2:00:00 PM
105	9:00:00 AM	11:50:00 AM	12:00:00 PM					2:00:00 PM
106	12:00:00 PM	1:40:00 PM	1:50:00 PM					4:00:00 PM
107	12:00:00 PM	1:50:00 PM	2:00:00 PM					4:00:00 PM
108	12:00:00 PM	2:00:00 PM	2:10:00 PM					4:00:00 PM
109	12:00:00 PM	2:10:00 PM	2:20:00 PM					4:00:00 PM
110	12:00:00 PM	2:20:00 PM	2:30:00 PM					4:00:00 PM
111	12:00:00 PM	2:10:00 PM	2:20:00 PM					5:00:00 PM
112	12:00:00 PM	2:20:00 PM	2:30:00 PM					5:00:00 PM
113	12:00:00 PM	2:30:00 PM	2:40:00 PM					5:00:00 PM
114	12:00:00 PM	2:40:00 PM	2:50:00 PM					5:00:00 PM
115	12:00:00 PM	2:50:00 PM	3:00:00 PM					5:00:00 PM
116	2:00:00 PM	4:10:00 PM	4:20:00 PM					7:00:00 PM
117	2:00:00 PM	4:20:00 PM	4:30:00 PM					7:00:00 PM
118	2:00:00 PM	4:30:00 PM	4:40:00 PM					7:00:00 PM
119	2:00:00 PM	4:40:00 PM	4:50:00 PM					7:00:00 PM
120	2:00:00 PM	4:50:00 PM	5:00:00 PM					7:00:00 PM

This is the code that I'm using, I know I'm missing something, I'm just not sure what. It's not lost on me that the solver scheduled 5 shifts and the max workforce needed in any timeframe is 5, but it's not enough to cover the workforce needs for the entire day.

# create shift matrix
df = num_workers_t_window.fillna(0).applymap(lambda x: 1 if x == "x" else x)
df = df.drop(columns = ["startTime"])
a = df.drop(columns =["T_Window","num_workers_required"]).values
number of shifts
n = a.shape[1]
number of time windows
T = a.shape[0]
of workers required per time window
d = df["num_workers_required"].values
labor hours per shift
w = shift_hours["Shift_Hours"].values.astype(int)
Decision Variables
y = LpVariable.dicts("num_workers", list(range(n)), lowBound=0, cat="Integer")
Create Problem
prob = LpProblem("Schedule_Creation", LpMinimize)
Minimize Labor Hours
prob += lpSum([w[j] * y[j] for j in range(n)])
Constraint for workers required in each time window
for t in range(T):
    prob += lpSum([a[t, j] * y[j] for j in range (n)]) >= d[t]
prob.solve()
print("Status:", LpStatus[prob.status])
for shift in range(n):
    print(
        f"The number of workers needed for shift {shift} is {(y[shift].value())} workers"
    )

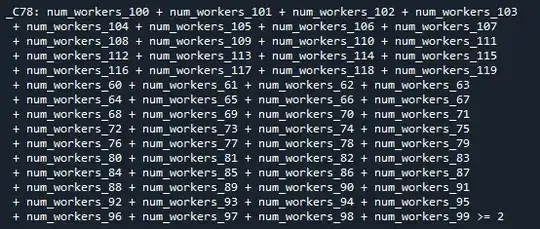
One of the constraints, per request in comments:

Adding the LP Model, source for this code is from this project: https://towardsdatascience.com/how-to-solve-a-staff-scheduling-problem-with-python-63ae50435ba4

Minimize function

Workforce requirement constraint

Adding a sample of data frame for shifts, workers required (last column), and associated time windows:

T_Window	Shift_1	Shift_2	Shift_16	Shift_17	Shift_31	num_workers_required
5:00:00 AM	1	1	0	0	0	1
5:10:00 AM	1	1	0	0	0	1
5:20:00 AM	1	1	0	0	0	1
5:30:00 AM	1	1	0	0	0	1
5:40:00 AM	1	1	0	0	0	1
5:50:00 AM	1	1	0	0	0	1
6:00:00 AM	1	1	1	1	0	2
6:10:00 AM	1	1	1	1	0	2
6:20:00 AM	1	1	1	1	0	2
6:30:00 AM	1	1	1	1	0	2
6:40:00 AM	0	1	1	1	0	2
6:50:00 AM	1	0	1	1	0	2
7:00:00 AM	1	1	1	1	1	3
7:10:00 AM	1	1	1	1	1	3
7:20:00 AM	1	1	1	1	1	3
7:30:00 AM	1	1	1	1	1	3
7:40:00 AM	1	1	0	1	1	3
7:50:00 AM	1	1	1	0	1	3
8:00:00 AM	1	1	1	1	1	4
8:10:00 AM	1	1	1	1	1	4
8:20:00 AM	1	1	1	1	1	4
8:30:00 AM	1	1	1	1	1	4
8:40:00 AM	1	1	1	1	0	4
8:50:00 AM	1	1	1	1	1	4
9:00:00 AM	0	0	1	1	1	4
9:10:00 AM	0	0	1	1	1	4
9:20:00 AM	0	0	1	1	1	4
9:30:00 AM	0	0	1	1	1	4
9:40:00 AM	0	0	1	1	1	4
9:50:00 AM	0	0	1	1	1	4
10:00:00 AM	1	1	0	0	1	4
10:10:00 AM	1	1	0	0	1	4
10:20:00 AM	1	1	0	0	1	4
10:30:00 AM	1	1	0	0	1	4
10:40:00 AM	1	1	0	0	1	4
10:50:00 AM	1	1	0	0	1	4
11:00:00 AM	1	1	1	1	0	4
11:10:00 AM	1	1	1	1	0	4
11:20:00 AM	1	1	1	1	0	4
11:30:00 AM	1	1	1	1	0	4
11:40:00 AM	0	1	1	1	0	4
11:50:00 AM	1	0	1	1	0	4
12:00:00 PM	1	1	1	1	1	4
12:10:00 PM	1	1	1	1	1	4
12:20:00 PM	1	1	1	1	1	4
12:30:00 PM	1	1	1	1	1	4
12:40:00 PM	1	1	0	1	1	4
12:50:00 PM	1	1	1	0	1	4
1:00:00 PM	1	1	1	1	1	5
1:10:00 PM	1	1	1	1	1	5
1:20:00 PM	1	1	1	1	1	5
1:30:00 PM	1	1	1	1	1	5
1:40:00 PM	1	1	1	1	0	5
1:50:00 PM	1	1	1	1	1	5
2:00:00 PM	1	1	1	1	1	4
2:10:00 PM	0	0	1	1	1	4
2:20:00 PM	0	0	1	1	1	4
2:30:00 PM	0	0	1	1	1	4
2:40:00 PM	0	0	1	1	1	4
2:50:00 PM	0	0	1	1	1	4
3:00:00 PM	0	0	1	1	1	4
3:10:00 PM	0	0	0	0	1	4
3:20:00 PM	0	0	0	0	1	4
3:30:00 PM	0	0	0	0	1	4
3:40:00 PM	0	0	0	0	1	4
3:50:00 PM	0	0	0	0	1	4
4:00:00 PM	0	0	0	0	1	3
4:10:00 PM	0	0	0	0	0	3
4:20:00 PM	0	0	0	0	0	3
4:30:00 PM	0	0	0	0	0	3
4:40:00 PM	0	0	0	0	0	3
4:50:00 PM	0	0	0	0	0	3
5:00:00 PM	0	0	0	0	0	2
5:10:00 PM	0	0	0	0	0	2
5:20:00 PM	0	0	0	0	0	2
5:30:00 PM	0	0	0	0	0	2
5:40:00 PM	0	0	0	0	0	2
5:50:00 PM	0	0	0	0	0	2
6:00:00 PM	0	0	0	0	0	1
6:10:00 PM	0	0	0	0	0	1
6:20:00 PM	0	0	0	0	0	1
6:30:00 PM	0	0	0	0	0	1
6:40:00 PM	0	0	0	0	0	1
6:50:00 PM	0	0	0	0	0	1

How would I grab just that portion of the constraint? I added a snip of one of the constraint iterations above. — t25, Feb 15 '22 at 17:38
What is the best way to pull that? Sorry, new to Pulp. Happy to put it up, just not sure how to grab it. — t25, Feb 15 '22 at 18:15
It is your mathematical model. Preferably as Text in latex format. If you dont know how to use latex then as image — PeterD, Feb 15 '22 at 18:19
I added it to the bottom. A lot of this is borrowed from a "Towards Data Science Article", link in the post. — t25, Feb 15 '22 at 18:30
Do your last lines of code only print the variables $y_0, y_{90}, y_{91}, y_{92}$? Or are the others just 0 and you did not want to show them? — PeterD, Feb 15 '22 at 19:44
It prints them all, but the body of the message was over the character count, so I removed them. All of the other variables return "0 workers" — t25, Feb 15 '22 at 20:35
Based on the left-side of your constraint, I would say that it is totaling up workers who are on from 4:50 to 5:00 pm. The right-hand side (2) is "num_workers_required" for 5:00 pm according to your data table. The "num_workers_required" for 4:50 pm is 3. Is it correct that "num_workers_required" is how many you need for the 10 minute segment ending at the specified time (as opposed to the segment starting at that time)? — prubin, Feb 16 '22 at 22:38
t is the start of the 10-minute time window. In the example you provided, from 4:50pm-5:00pm, 3 workers are needed. Then from 5:00pm to 5:10pm, 2 workers are needed. — t25, Feb 16 '22 at 22:46
Then you might want to check the code that generates $a_{jt}$ to see if it conforms to that convention. The left side of your constraint contains shift that end at 5:00, so comparing their sum to the demand for 5:00-5:10 is wrong. — prubin, Feb 16 '22 at 23:29
a, n, t, and d all originate from the same data frame, so they all use the same time scale. Given that, how could they be comparing different time frames on the left and right sides? — t25, Feb 17 '22 at 14:59
I agree with @prubin, I suspect there is problem with $a_{jt}$. In particular, there seems to be a difference in granularity between the demands and the shifts. Could you attach the df in csv so that we can replicate ? — Kuifje, Feb 17 '22 at 17:08

Kuifje · Accepted Answer · 2022-02-21T15:01:24.177

First, it is confusing when you say

The final solution does not satisfy the workforce requirements for the various time windows, it's substantially short. Only 5 shifts are filled in total.

You do not want to fill in shifts, but time windows. You select shifts in order to satisfy workforce requirements for each time slot.

I suspect you have some issues with your shifts, when you translate them from the format

Shift_Num	Start_Shift	First_Break_Start	First_Break_End	Lunch_Start	Lunch_End	Second_Break_Start	Second_Break_End	End_Shift

to the format with $10$ min time slots. For example, shift $1$ should be (if I am not mistaken) :

Addendum

With the table of shifts added by the OP, removing the set of time slots which cannot be covered at all (after 4:00 PM), and with $w_j=1$ for $j=1,2,16,17,31$, I get a total of 9 shifts (shift $2$, shift $17$ (4 times), and shift $31$ (4 times)):

Here is the code I used (shifts.csv is a csv file with shifts OP posted in the last table):

import pulp
from pandas import read_csv
df = read_csv("shifts.csv", sep=";")
a = df.drop(columns=["num_workers_required"]).values
number of shifts
n = a.shape[1]
number of time windows
T = a.shape[0]
of workers required per time window
d = df["num_workers_required"].values
labor hours per shift
w = shift_hours["Shift_Hours"].values.astype(int)
Decision Variables
y = pulp.LpVariable.dicts("num_workers", list(range(n)), lowBound=0, cat="Integer")
Create Problem
prob = pulp.LpProblem("Schedule_Creation", pulp.LpMinimize)
Minimize Labor Hours
prob += pulp.lpSum([y[j] for j in range(n)])
Constraint for workers required in each time window
for t in range(T):
    prob += pulp.lpSum([a[t, j] * y[j] for j in range(n)]) >= d[t]
prob.solve()
print("Status:", pulp.LpStatus[prob.status])
for shift in range(n):
    print(
        f"The number of workers needed for shift {shift} is {(y[shift].value())} workers"
    )

And here is the output:

Addendum 2

With this data (and $w_j=1$ for every shift $j$), I get the following optimal solution: shifts 15, 36, 91 (twice), 94, i.e., 5 shifts. This solution is not unique. And this solution is feasible, as the orange line always lies above the blue line in the Figure below:

I think part of the confusion may come from the fact that in the data, the index of the first shift is $1$, while it is $0$ in the python code. So when the solver selects shifts 14, 35, 90, 93, it is actually pointing to shifts 15, 36, 91, 94 in the file with the raw data.

Comments are not for extended discussion; this conversation has been moved to chat. — ə̷̶̸͇̘̜́̍͗̂̄︣͟, Feb 21 '22 at 21:04
Marking this as the answer. This helped me resolve a number of issues. A significant source of my issue was a problem with the source shift file, which this analysis helped identify. — t25, Feb 23 '22 at 07:38

PeterD · Answer 2 · 2022-02-16T08:54:48.090

2

You expect $y_j > 0$ for every $j$. Looking at the LP however, this does not need to be the case. Just the sum $y_j * a_{jt}$ over every $j$ needs to fulfill your demand for every $t$ (i.e. be at least 1). Your pulp code seems to be right and also the solution it gives is (most likely) valid.

edited Feb 16 '22 at 08:54

answered Feb 16 '22 at 08:15

PeterD

1,501
4
16

y(j) needs to be >= 0 for every j (can have 0 workers, but can't have negative workers). Unfortunately, the solution is not valid, I've manually validated it and it's missing substantial headcount. – t25 Feb 16 '22 at 15:10
I'm thinking the problem may be that there are shifts that cover the same t period with different break schedules, which is why y(j) could potentially be equal to zero if it is not optimal to schedule workers on that shift to meet the demand for every t. Something in that logic is not working correctly, it may even be wrong in my LP and I'm just not accounting for that correctly. – t25 Feb 16 '22 at 15:24
That might be true. I can just state that the pulp implementation of your LP is correct. – PeterD Feb 16 '22 at 15:46

Python Pulp - LpMinimize Not Returning Expected Output - Scheduling Problem

number of shifts

number of time windows

of workers required per time window

labor hours per shift

Decision Variables

Create Problem

Minimize Labor Hours

Constraint for workers required in each time window

2 Answers2