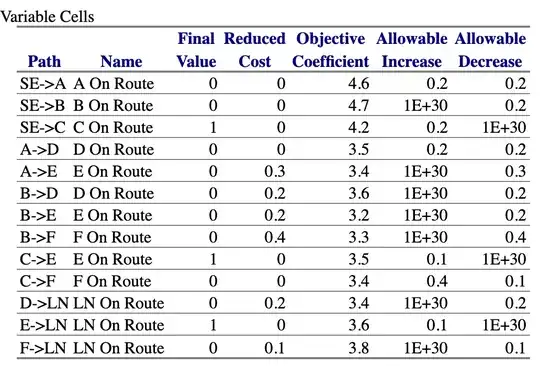
In solving a linear program (in specific a network optimization problem of the shortest path type) with the Excel solver, I noticed two things after running a sensitivity report on the solution suggested by the solver:
First, both the allowable increase as well as the allowable decrease were positive for all variables, which indicates that the solution suggested is a unique optimal solution.
Second, the final value as well as the reduced cost were both 0 for multiple variables, which usually indicates that these variables are part of another Corner Point Feasible solution at another optimal corner.
These two observations obviously contradict one another, which is quite confusing. The solution is definitely the only optimal solution for the problem.
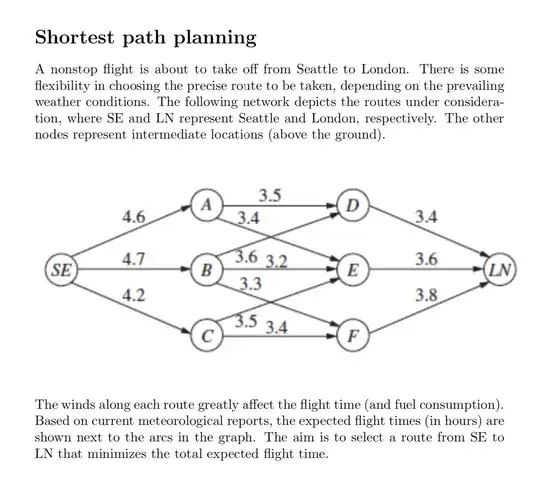
Presented below are the optimization problem and the Sensitivity Report. The objective was to find the shortest path from SE to LN.