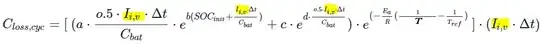[EDIT] : The formula below is updated to remove the radical, 0.5 in the term $(I_{i,v} \cdot \Delta t)$ and constant temperature $T$ replces temperature as function of current.
[EDIT] :The values of the constants are added
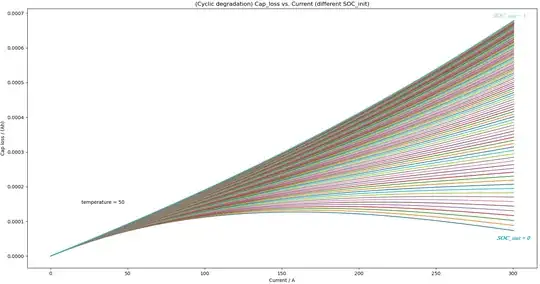
[EDIT] : Plot of $$ C_{loss,cyc} \ Versus \ I_{i,v} \ \ \ \ for \ \ SOC_{init} \in [0,1]$$ is shown below. Is it possible to approximate these family of functions using a simpler function like $$(1 - e^{-x})$$ ? Could you please suggest some functions?
[EDIT] : I have added the constraints to the problem below. Constants in the constraints are $$ I_{max}, I_{c,max}, T^{dep}_{v},t_s, SOC^{dep}_{v}, SOC_{-1,v}, SOC_{xtra}$$
I would like to minimize the following objective function.
\begin{equation} \min_{I_{i,v}} \ \sum^{N_v}_{v}\sum^{TT_v}_{i} \ C_{loss,cyc} \end{equation}
where the expression for $C_{loss,cyc}$ is described below.
The following are constants: $$ a = -4.092 \cdot 10^{-4} , b = -2.167 , c = 1.408 \cdot 10^{-5}, d = 6.130, E_a = 7806, R = 8.3145 , T_{ref} = 28, \Delta t = 0.1, SOC_{init} \in [0,1], C_{bat} = 270, T = 50 $$
The only continuous decision variable is $ I_{i,v}$ It is highlighted below
[EDIT] : Explaination of the optimization problem.
In a charging station, that has $N_v$ vehicles that needs to be charged to some state of charge $SOC^{dep}_v$ within some departure time $T^{dep}_v$. The charging schedule for each vehicle,v is thus split into timeslots, i of width $\Delta t$ each for $TT_{v}$ number of slots. Within a timeslot, i the current $I_{i,v}$ is constant. $t_s $ is just starting time of optimization implementation. The objective is trying to minimize the Electric vehicle's battery capacity loss.
I want to perform linearlization of the objective function in order to achieve near real-time performance for one hundred decision variables in an optimization problem.
I know about first order taylor approximation but what are some of the other methods I can use especially with regards to this type of objective function with exponential and power terms to linearlize it.
You can also suggest any similifications to this model. If there is another way to solve this quickly without having to linearize it. Please suggest as well.
Assume that our solver is NOT the best so we need to simplify the model mathematically to compensate for the solvers shortcomings.