8

I am currently working on weighted perfect bipartite matching, i.e., assignment problem.

Formally speaking, it could be formulated as follows:

$$ min \sum\limits_{i=1}^{N}\sum_{j=1}^{N}c_{ij}x_{ij} $$ , where $$ \sum\limits_{j=1}^{N}x_{ij} = 1 (i=1...N),\\ \sum\limits_{i=1}^{N}x_{ij} = 1 (j=1...N),\\ x_{ij}\in \{0,1\} $$ Here, $c_{ij}\in R$ is given as the cost matrix.

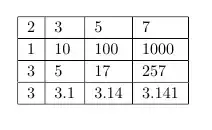
But now, my problem has an additional constraint on it : $c_{ij} < c_{ij'}$ if $j < j'$.

That is, each row of the cost matrix is monotonically increasing. For example, the following cost matrix:

cost matrix

(By analogy with workers and jobs, it is like that jobs in right is more difficult so every workers needs more time to get it done.)

The classic Kuhn-Munkres algorithm can be used to solve assignment problem and it can be applied to this surely. But I wonder if any faster algorithm (or related research) exists. I have tried some greedy approaches but it doesn't seem to work.

Thanks!!

prubin
  • 39,078
  • 3
  • 37
  • 104
Shinshin
  • 83
  • 3

1 Answers1

8

I don't think the monotonicity will help much, for the following reason. Start with any arbitrary assignment problem. Add a constant amount $K$ to $c_{i2}$ for all $i$, with $K$ sufficiently large to make $c_{i2} > c_{i1}$ for all $i$. Since someone has to be assigned to sink 2, this effectively adds a constant amount $K$ to the objective function, and so any optimal solution to the modified problem will be optimal in the original problem (and vice versa). Now repeat, adding a (different) constant amount to each column of the cost matrix to make it bigger than the previous column, until the monotonicity condition is satisfied.

What this shows is that every assignment problem is equivalent (in the sense of having exactly the same feasible region and exactly the same set of optimal solutions) to an assignment problem satisfying the monotonicity condition. If someone had found a way to exploit monotonicity, it would be used for all assignment problems. As far as I know, there is no such algorithm for the general assignment problem.

prubin
  • 39,078
  • 3
  • 37
  • 104
  • Brilliant! In that way, every general assignment problem can be reduced to a "monotonic" version AP. Thanks for clear explanation. – Shinshin Sep 18 '21 at 07:01