In which time complexity operates the Savings algorithm from Clarke and Wright for the TSP? I mean the parallel version of Savings. I think it is in $\mathcal O(|V|\log|V|)$ with V as vertex/node because the most complex operation is sorting the savings which operate in this time for, e.g. Quicksort. The rest operates, I think, in linear time. Is this right, and is there something on the internet that covers this?
Asked
Active
Viewed 363 times
1 Answers
4
You might want to read the paper DIFFERENT VERSIONS OF THE SAVINGS METHOD FOR THE TIME LIMITED VEHICLE ROUTING PROBLEM[1] which gives time complexities between $O(n^3)$ and $O(n^2\log(n))$ note that in these complexity analysis the number of nodes not nodes as $n$. The reason why it is $n^2$ and not $n$ is this part of the algorithm:
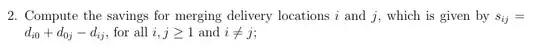Taken from EOR 151 – Lecture 18 Savings Algorithm page 1
The number of savings grows $O(n^2)$ (actually like $n(n+1)/2$) so sorting that leads to $O(n^2\log(n^2)) = O(2n^2\log(n)) = O(n^2\log(n))$ time complexity unless a non-comparison based sorting like trie/radix/couting sort is used.
worldsmithhelper
- 4,007
- 6
- 21
-
V is the set of vertices or nodes. So n=|V|. This would not agree with the complexity that I proposed. Why does the sorting take longer than O(|V|log|V|)? – maxmitz Sep 17 '21 at 07:41
-
Sorry i confused vertices for edges. – worldsmithhelper Sep 17 '21 at 07:47
-
1@Theodeo my newest edit should make it clear while sorting takes $O(|s|*log(|s|))$ where $|s|$ is the number of savings and $|s|$ is in $O(n^2)$ – worldsmithhelper Sep 17 '21 at 07:58