7

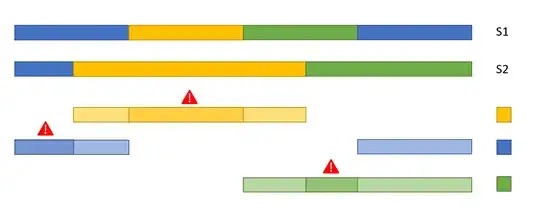
I'm given a problem in which I need to schedule multiple sequences. The goal is to minimize the makespan. I'm allowed to elongate all tasks, but I cannot reduce their width nor disconnect any of the tasks. Each of the tasks is indicated using a color. In the final schedule tasks of the same color cannot overlap. Example task illustration with colors

In the example above 2 sequences S1, S2 are shown with respectively 4 and 3 tasks in 3 different colors. In the example both tasks are scheduled to start at the same time but this results in 3 violations. These violations are indicated by an exclamation mark.

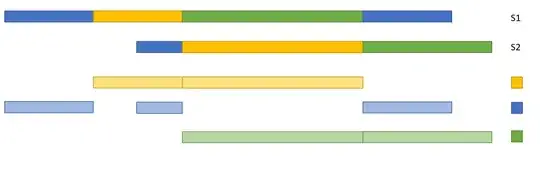
The optimal solution for this example would be to elongate the green task of S1 and align them as seen in the optimal solution below. Optimal Solution

Is this type of problem known and studied in literature? If so, under what name and what kind of algorithms are used to solve them? If not, what kind of algorithm would you suggest to use? I have +- 100 sequences and I am using 16 colors. Each sequence contains typically between 9 and 20 tasks.

I found many problem types where disconnecting the tasks within a sequence is allowed, but not being able to disconnect changes the dynamics quite a bit.

Barry S.
  • 73
  • 4
  • 1
    Welcome to OR.SE. First of all, what do you mean by schedule multiple sequences? From the practical overview, scheduling and sequencing are the same concepts. Would you provide more details about your problem? E.g. each task is independent or does have to sub-operations? Are there any precedence constraints or something like a route for each one?

    Without losing generality, your problem can be categorized into the parallel machine scheduling problem. If you could provide more information, it gives more chance to answer your question by the community. :)

     – A.Omidi Aug 25 '21 at 11:52
  • In the example you can find 2 sequences (as intended), S1 contains out of 4 tasks, S2 contains out of 3 tasks. Due to the color of each of the tasks and the connected sequence constraint a lot of dependencies arise. Within each sequence the order needs to be preserved, so this does create precedence constraints and routing constraints on the task level. – Barry S. Aug 25 '21 at 12:00
  • So you already have the two ordered sequences S1 and S2, and all you want to do is add "downtime" inside the sequences to avoid collisions of incompatible tasks? – Stef Aug 25 '21 at 12:19
  • @Barry S., are what you looking for is something like this? – A.Omidi Aug 25 '21 at 12:22
  • @Stef, Yes! Though my initial problem has over 100+ sequences instead of 2. – Barry S. Aug 25 '21 at 12:33
  • @A.Omidi, more or less. Each sequence can start/end at any moment in time. It's just that the tasks cannot be disconnected and several sequences can create conflicts if the tasks with identical color overlap. – Barry S. Aug 25 '21 at 12:33
  • @BarryS., would you say please, in my initial schedule which tasks are being overlapped or disconnected? – A.Omidi Aug 25 '21 at 12:44
  • @BarryS. Have you tried the greedy approach of delaying tasks if a conflicting task is already started? – Stef Aug 25 '21 at 12:50
  • @A.Omidi In your example, each of the tasks has a different color (so by default no violations). If you'd consider all Greens to be the same color (J001, J005, J015, J009, J017), you have 3 violations. One between J005, J015; one between J009, J017 and a final one between 001, J017 – Barry S. Aug 25 '21 at 12:52
  • 1
    @BarryS. Based on the conversations happening here in the comments, I suggest you edit your question and add these clarifying points and any other details there. – EhsanK Aug 25 '21 at 12:56
  • If you consider each sequence as one task and each color as a resource, then the problem becomes a resource constrained scheduling problem (without considering the elongation) – fontanf Aug 25 '21 at 12:56
  • @BarryS., please be aware that, the problem I mentioned is a parallel machine scheduling problem. It means each sequence of the tasks is being performed by a specific resource, Uno.01, Uno.02, Uno.03, and what you actually see is not overlap nor disconnect. I agree with EhsanK to clarify your question. :) – A.Omidi Aug 25 '21 at 13:05
  • @BarryS. Using the blue task as an example, you currently have it in three pieces. Is it correct that you can chop it into as many or as few (say, one) pieces as you like, so long as the combined width of the pieces meets or exceeds some specified limit (and other constraints, including no overlap, are satisfied)? – prubin Aug 25 '21 at 15:47
  • Out of curiosity, may I know if there is a real world application that motivated your problem, and if yes, can you briefly mention it? – batwing Aug 27 '21 at 15:31
  • @batwing I'm working on a scheduling problem where a single robotic-arm is facilitating all adjacent machines. Since the machines and the robotic arm all have capacity 1, I paraphrased it to the colors since this is much more visually understandable. The idea is to extend this problem for multiple robotic workcells that can interact with other cells by AGVs that move parts etc. I hope this gives sufficient amount of clarity. – Barry S. Sep 01 '21 at 14:16

2 Answers2

5

This is a blocking job shop scheduling problem.

The description from "An iterated greedy metaheuristic for the blocking job shop scheduling problem" (Pranzo et Pacciarelli, 2016) DOI

In the job shop scheduling problem a set of jobs $J$ must be processed on a set of machines $M$, each processing at most one job at a time. The processing of a job on a machine is called an operation and cannot be interrupted. We let $\{o_1, \dots , o_n \}$ be the set of all operations. The sequence of operations for each job is prescribed, while the sequence of operations for each machine has to be determined in such a way that the time needed to complete all operations, called the makespan, is minimum. More formally, the scheduling problem consists in assigning a starting time $t_i$ to operation $o_i$ , $i = 1, \dots, n$, such that: (i) precedence constraints between consecutive operations of the same job are satisfied; (ii) each machine hosts at most one job at a time; and (iii) the makespan is minimized.

In the blocking job shop scheduling problem no intermediate storage is allowed between two consecutive machines. Hence, once a job completes processing on machine $M_h$ it either moves to the subsequent machine $M_k$ (if it is available) or it remains on $M_h$, thus blocking it (if $M_k$ is not available).

From your examples, "sequences" become "jobs", "tasks" become "operations", and "colors" become "machines".

The simplest and easiest way to get solutions is certainly to use a Constraint Programming solver.

fontanf
  • 2,623
  • 6
  • 11
  • would you say please, how this problem might be fallen into the job shop scheduling problem? – A.Omidi Aug 28 '21 at 05:47
  • @A.Omidi What do you mean? As I've written in the answer the colors are resources with capacity 1, that is, equivalent to machines. Sequences and tasks are jobs and operations. Elongating an operation (task) is equivalent to saying that while the next operations of that job (sequence) has not started, the machine (color) of the previous operation is still busy. This is the "blocking" property – fontanf Aug 29 '21 at 07:15
  • As the questioner does not mention anything about either the specific route for each task or sub-operations that is required and necessary for scheduling the shopping environments, I doubt this problem can be categorized in the JSSP. Maybe an open shop or parallel machine scheduling is more suitable. Do you have any reference to use JSSP in other environments like PMSP/RCPS? – A.Omidi Aug 29 '21 at 07:31
  • @A.Omidi the route is the sequence. From what I understand, it is not possible to change the order of the colors in a sequence, therefore it's a JSSP. Otherwise, I agree that it would be an open shop scheduling problem – fontanf Aug 29 '21 at 08:55
  • The route is a bit different from the sequence, specifically, for the non-shopping environments. It's a key point in the practical sequencing problem. For example, in the PMSP with two resources, without any limitation based on the Graham notation, a feasible sequence of the four jobs on the resource one would be => [j1, j3] and for the second one would be => [j2, j4] and this is not meaning as a route. :) – A.Omidi Aug 29 '21 at 09:21
  • I'm not sure that we use the same vocabulary. By route, I mean the precedence chain of the operations of a job: $o_{1,1} \to o_{1,2} \to o_{1,3}$. By sequence, I mean how they are described in the question. Here, if a sequence $S_1$ is made of three tasks $T_{1,1}$, $T_{1,2}$ and $T_{1,3}$, this is equivalent to a job with three operations following the route $o_{1,1} \to o_{1,2} \to o_{1,3}$. – fontanf Aug 29 '21 at 10:26
  • The "sequences" of the question are not exactly what is called "sequence" in the scheduling literature. Maybe that's why there is a confusion. But I'm pretty sure that I understood what op meant – fontanf Aug 29 '21 at 10:31
  • I totally agree with what you mentioned about the route in the previous comment. This rises in the shopping problem where each task does have sub-operations. In the above question, as the OP did not mention anything about the route or sub-operations of a task, I am interested to ask you how you could classify this question as a JSSP. – A.Omidi Aug 29 '21 at 11:25
  • OP did not use the word "route", but the routes are what is called sequences in the question. And what is called tasks in the question is actually the sub-operations – fontanf Aug 29 '21 at 11:49
  • What you could understand from the question is interesting. :) – A.Omidi Aug 29 '21 at 12:30
1

Your problem is reminiscent of the makespan minimization version of the Blocking Job Shop (BJS) problem. For a definition of the BJS problem, refer to [1]. If you consider each sequence as a job, and each color as a machine, then, it looks like the problem sizes that you are interested in are pretty large, and so local-search may be your best bet to compute good quality solutions. For local-search algorithms to solve the BJS problem efficiently, see the recent paper [2].

[1] "Job-shop scheduling with blocking and no-wait constraints", Alessandro Mascisa & Dario Pacciarelli, EJOR, 2002.

[2] "Efficient primal heuristic updates for the blocking job shop problem", JK Mogali, L Barbulescu, SF Smith, EJOR, 2021.

batwing
  • 1,458
  • 6
  • 15