Prove that these linear programming problems are bounded by $O(k^{1/2})$

Question

Prove that these linear programming problems are bounded by $O(k^{1/2})$

Conjecturally the expanded partial sums of the Möbius transform of the Harmonic numbers have two out of three properties in common with this set of linear programming problems:

$$\begin{array}{ll} \text{minimize} & \displaystyle\sum_{n=1}^{n=k} \frac{x_{n}}{n} \\ \text{subject to constraints:} & k + \displaystyle\sum_{n=2}^{n=k}x_{n}=1 \\ & x_1 \geq -1 \end{array}$$

for all $k$ and for $n>1:$

$$-2(n-1) \leq x_n \leq 0 \tag{4}$$

That is, there is one linear programming problem for each $k$.

The sequence I get is: $${-(1/2), -1, -(4/3), -(5/3), -2, -(7/3), -(31/12), -(17/6), -(37/ 12), -(10/3), -(43/12), -(23/6), -(121/30), -(127/30), -(133/30), -( 139/30), -(29/6), -(151/30), -(157/30), -(163/30), -(28/5),...}$$

Based on a OEIS search, the solutions $f(k)$ to the linear programming problems (without the first column) appear to have the asymptotic:

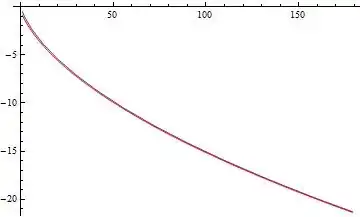
$$f(k)=-\left(2 \sqrt{k}-2 \log \left(\sqrt{k}+1\right)-2 \gamma +1\right) \tag{5}$$ Is it true?

Please don't be so harsh on me. If the problem is ill defined in the latex I post the short Mathematica program from which I defined the optimization problem.

(*start*)
nn = 180;
TableForm[
  L2 = Table[
    LinearProgramming[
     Table[1/n, {n, 1, k}], {Table[If[n == 1, k, 1], {n, 1, k}]}, {{1,
        0}}, Table[
      If[n == 1, {-1, 1}, {-2 (n - 1), 0 (n - 1)}], {n, 1, k}]], {k, 
     1, nn}]];
t1 = Table[Sum[L2[[n, k]]/k, {k, 2, n}], {n, 2, nn}];
t2 = Table[-(2*k^(1/2) + 1 - 2*Log[k^(1/2) + 1] - 2*EulerGamma), {k, 
    2, nn}];
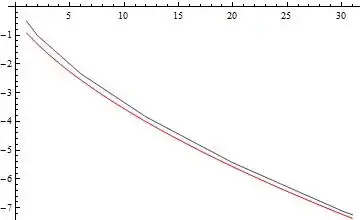
Show[ListLinePlot[t1], ListLinePlot[t2, PlotStyle -> Red]]
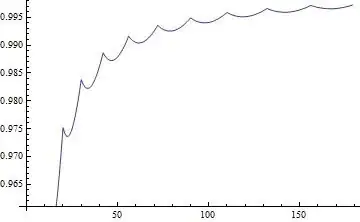
ListLinePlot[t1/t2]

The blue curve is the linear programming minimum and the red curve is the asymptotic.

Zoom in:

The ratio between the linear programming minimum and the asymptotic tends to one.

So as I said this is NOT a bound on the partial sums of the Möbius inverse of the Harmonic numbers.

The solutions $x_1,\cdots,x_k$ to the $k$-th linear programming problem form a number triangle:

$$\begin{array}{llllllllllll} 1 & \text{} & \text{} & \text{} & \text{} & \text{} & \text{} & \text{} & \text{} & \text{} & \text{} & \text{} \\ 1 & -1 & \text{} & \text{} & \text{} & \text{} & \text{} & \text{} & \text{} & \text{} & \text{} & \text{} \\ 1 & -2 & 0 & \text{} & \text{} & \text{} & \text{} & \text{} & \text{} & \text{} & \text{} & \text{} \\ 1 & -2 & -1 & 0 & \text{} & \text{} & \text{} & \text{} & \text{} & \text{} & \text{} & \text{} \\ 1 & -2 & -2 & 0 & 0 & \text{} & \text{} & \text{} & \text{} & \text{} & \text{} & \text{} \\ 1 & -2 & -3 & 0 & 0 & 0 & \text{} & \text{} & \text{} & \text{} & \text{} & \text{} \\ 1 & -2 & -4 & 0 & 0 & 0 & 0 & \text{} & \text{} & \text{} & \text{} & \text{} \\ 1 & -2 & -4 & -1 & 0 & 0 & 0 & 0 & \text{} & \text{} & \text{} & \text{} \\ 1 & -2 & -4 & -2 & 0 & 0 & 0 & 0 & 0 & \text{} & \text{} & \text{} \\ 1 & -2 & -4 & -3 & 0 & 0 & 0 & 0 & 0 & 0 & \text{} & \text{} \\ 1 & -2 & -4 & -4 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \text{} \\ 1 & -2 & -4 & -5 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{array}$$

The first column is here equal to the all ones sequence because Mathematicas linear programming command seems to require it. But setting the constraint to begin with $k$ (in the linear program in the beginning of the question) makes it equivalent to the first column in the numerators for partial sums of the Möbius inverse of the Harmonic numbers.

Counting only the negative entries in each row we find with a OEIS search that their number appear to be nearest integer to square root of $n$, and from there it becomes easy to conjecture formula $(5)$.

The partial sums of the Möbius inverse of the Harmonic numbers have the numerators:

$$J(m,k)=\begin{array}{lllllll} 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 2 & -1 & 0 & 0 & 0 & 0 & 0 \\ 3 & 0 & -2 & 0 & 0 & 0 & 0 \\ 4 & -1 & -1 & -1 & 0 & 0 & 0 \\ 5 & 0 & 0 & 0 & -4 & 0 & 0 \\ 6 & -1 & -2 & -1 & -3 & 2 & 0 \\ 7 & 0 & -1 & 0 & -2 & 3 & -6 \end{array}$$

given by the sum:

$$\sum _{n=1}^m \text{If}[n\geq k,a(\gcd (n,k)),0]$$

for
$n=1,\cdots,m$,
$k=1,\cdots,N$,
$m=1,\cdots,N$. and where $a(n)$ is the Dirichlet inverse of the Euler totient function.

The properties are:

$$\sum_{k=1}^{k=n} \frac{J(n,k)}{k}=\sum _{k=1}^n \text{If}\left[n \bmod k=0,H_k \mu \left(\frac{n}{k}\right),0\right]$$ which is the partial sums of the Möbius inverse of the m-th harmonic number

$$\sum_{k=1}^{k=n}J(n,k)=1$$ as in the constraint in the linear programming problem. $$J(n,1)=n$$ as in the linear programming problem (but in the linear programming problem it is in the constraint and not the goal function because of some Mathematica technicality.)

The last property, for all $n$:

$$-2(k-1) \leq J(n,k) \leq 2(k-1)$$

is conjectural and differs from the linear programming problem. This last conjectural property should not be too hard to prove.

(*Numerators of the partial sums of the Möbius inverse of the \
Harmonic numbers*)(*start*)
Clear[T, n, k, a];
nn = 7;
a[n_] := If[n < 1, 0, Sum[d MoebiusMu@d, {d, Divisors[n]}]]
TableForm[
 M = Table[
   Table[Sum[If[n >= k, a[GCD[n, k]], 0], {n, 1, m}], {k, 1, nn}], {m,
     1, nn}]]
Table[Sum[M[[n, k]]/k, {k, 2, n}], {n, 1, nn}] (*<--sequence to be bounded*)
(*end*)

Previously asked yesterday at Mathematics stack exchange, where I was not understood. I also asked about the notation at Mathematica stack exchange. And I also asked it at mathoverflow but was sent here.

---

Edit 14.10.2019:

In other words this linear programming problem is valid for the partial sums of the Möbius inverse of the Harmonic numbers:

$$\begin{array}{ll} \text{minimize} & \displaystyle\sum_{n=1}^{n=k} \frac{x_{n}}{n} \\ \text{subject to constraints:} & k + \displaystyle\sum_{n=2}^{n=k}x_{n}=1 \\ & x_1 \geq -1 \end{array}$$

for all $k$ and for $n>1:$

$$-2(n-1) \leq x_n \leq 2(n-1)$$

Edit: 24.10.2019

Keyword(s) for Google searches: Square root bound

Edit 13.4.2020:

(*start*)
Clear[A];
nn = 20;
L = LinearProgramming[
   Flatten[Table[Table[1/k, {k, 1, n}], {n, 1, nn}]], 
   Table[Flatten[
     Table[Table[If[n == i, 1, 0], {k, 1, n}], {n, 1, nn}]], {i, 1, 
     nn}], Table[{1, 0}, {n, 1, nn}], 
   Flatten[Table[
     Table[If[k == 1, {n, n}, {-(k - 1), (k - 1)}], {k, 1, n}], {n, 1,
       nn}], 1]];
TableForm[
 A = Table[Take[L, {n*(n - 1)/2 + 1, n*(n + 1)/2}], {n, 1, nn}]]
(*end*)

Answer 1

Your linear program is similar to a mathematical formulation of a bounded Knapsack problem and has a similar linear relaxation.

First note that $x_1$ is only restricted by $x_1\geq -1$ and thus $x_1=-1$ at optimality. The sum of remaining variables is bounded by $1-k$ (indeed has to be equal to $1-k$) and since variables with lower indices have higher value in the objective function, each variable in order of increasing indices will be at its lower bound at optimality, until hitting the bound, with the possible exception of the last variable.

In particular for $k=3,7,13,\cdots,\ell(\ell+1)+1$, with $\ell=1,2,\cdots$ the optimal solution has variables $x_1,x_2,\cdots,x_{\ell+1}$ at their lower bounds and the remaining variables at $0$. The objective value for these solutions is \begin{align*} \sum_{i\in I}\frac{x_i}i = -1 +\sum_{i\in I} \frac{-2(i-1)}i = -1 - 2 \sum_{i\in I}\left(1-\frac1i\right)= 2\left(H_{\ell+1}-(\ell+1)\right)-1 \end{align*} where $I=[2,l+1]$.

The sequence you give seems to ignore the contribution $-1$ for $x_1$, so for asymptotics we look at $2\left(H_{\ell+1}-(\ell+1)\right)$. Substituting $\ell=(\sqrt{4k-3}-1)/2$ you get \begin{align*} 2\left(H_{(\sqrt{4k-3}+1)/2}-(\sqrt{4k-3}+1)/2\right)\approx\ln(4k-3)-2\ln 2+2\gamma-(\sqrt{4k-3}+1) \end{align*} using $H_n\approx\ln n+\gamma$.