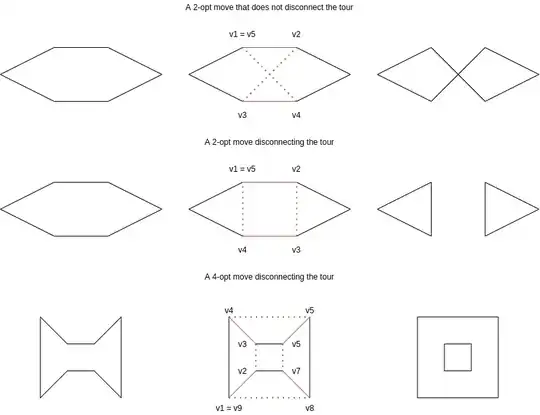
Given a current solution $S$ and a $k$-exchange move $(v_1, .., v_{2k+1})$ with $v_1 = v_{2k+1}$, $v_i \neq v_j$, $(v_i, v_{i+1}) \in E(S)$ iff $i$ odd, i.e. we remove all edges $(v_i, v_{i+1})$ for $i$ odd and add all edges $(v_i, v_{i+1})$ for $i$ even. Is there a way to determine in $O(k)$ if the move is feasible, i.e. if the resulting solution is connected?
To illustrate the question, here are a couple of examples: