5

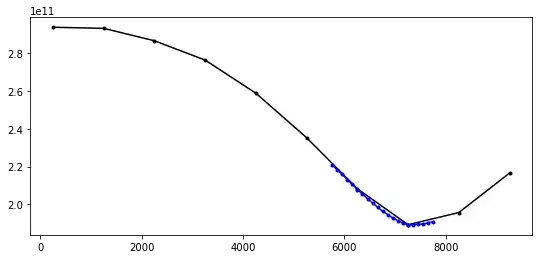
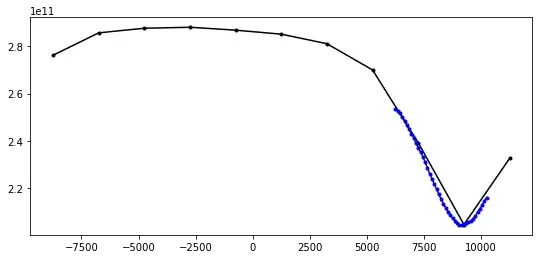
I need to solve a series of single parameter black-box minimization problem. The underlying cost functions are quite simple. They always have the same shape: a global minimum inside a fixed interval (-15000; 15000).

The constraints are :

  • The function is not differentiable;
  • The function is slow to evaluate.

I can solve these problems using a coarse scan followed by a fine scan. But I need between 30 and 50 evaluations. I'm sure that there is a better way to do it, but I can't find how.

Two examples of these cost functions :

enter image description here enter image description here

Kh4zit
  • 175
  • 1
  • 4

2 Answers2

5

Given that your function is apparently unimodal (single local minimum, which is global), you might try golden section search. The first four function evaluations result in about a 40% reduction in the initial interval. Each additional function thereafter again reduces the remaining interval by about 40%.

prubin
  • 39,078
  • 3
  • 37
  • 104
2

I would advise Bayesian Optimization. The benefits imho are that they don’t require a gradient, work for a wide variety of optimization problems and are made for when we are dealing with functions that are hard or slow to evaluate.

ə̷̶̸͇̘̜́̍͗̂̄︣͟
  • 5,412
  • 5
  • 22
  • 55
Steven01123581321
  • 1,043
  • 6
  • 12