1

I have the following problem which seems to be a mixture of a resource constrained scheduling and packing problem.

There is a set of activities $A_1,\ldots,A_n$ and given precedences $P$, where $(A_i,A_j)\in P$ means $A_i$ needs to run before $A_j$. There is a set of machines $M_1,\ldots,M_k$. Any activity can be run on any machine. Each $A_i$ has a certain resource consumption on a machine.

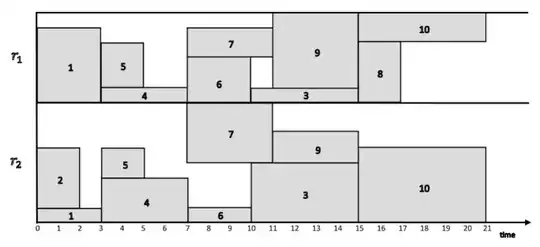
Here the packing aspect comes into play. Any machine can be viewed as a rectangle where the $x$-coordinate is time and the $y$-coordinate is the amount of a resource. Any activity $A_i$ has a resource consumption characterized by an area $c_i$. Say, if $A_1,\ldots,A_3$ are scheduled on $M_1$ then we have to place rectangles $r_1,\ldots,r_3$ of areas $c_1,\ldots,c_3$ into the rectangle of $M_1$ without overlap. The goal is to schedule each task on a machine such that the least amount of time has elapsed. This is equal to minimizing the maximum $x$-coordinate of the machines where there is no activity to the right.

In a further variant it is also possible that for a activity $A_i$ we can place multiple rectangles $r_{i1},\ldots,r_{ij}$ into the big rectangle of a machine, such that the areas of those rectangles sum up to $c_i$. But there is also the restriction that $r_{i1},\ldots,r_{ij}$ do not have gaps with respect to the $x$-coordinates and must be scheduled to the same machine.

ə̷̶̸͇̘̜́̍͗̂̄︣͟
  • 5,412
  • 5
  • 22
  • 55
Daniel Binkele-Raible
  • 19
  • 1
  • Are you saying that a machine can work on multiple activities (these are usually known as "tasks" in the scheduling literature) simultaneously, so long as the concurrent resource consumption stays below the amount available at the machine? – prubin May 13 '21 at 20:11
  • Yes, that is the case. A machine can accommodate multiple activities ("tasks") at the same time, just as long there is enough resource available. And of course resource consumption is measured in a discrete way. – Daniel Binkele-Raible May 14 '21 at 04:16

2 Answers2

3

I'm not sure there is name for your specific problem, but I think it is safe to say that it falls into the umbrella category of job shop scheduling, with the objective of minimizing makespan. If you do a web search for "taxonomy of job shop models" you will find a barely finite number of diagrams and articles on the subject. This paper, for instance, gives some structure the general subject.

Both integer programming models and constraint programming models are commonly used for problems such as yours. I will note, among the various options, that IBM's CP Optimizer constraint solver has global constraints specifically designed for scheduling problems, including one or more that let you model resources that can be shared by simultaneous tasks as long as their collective demand for the resource does not exceed supply. (Supply can vary with time.)

prubin
  • 39,078
  • 3
  • 37
  • 104
  • Indeed, the precedence constraints and the multi-machine environment makes it related to a flexible job shop. The resource component makes it related to Resource Constrained Project Scheduling Problems (RCPSP). I might be worth mentioning it too. I don't know if there is something about multi-machine RCPSPs in the literature – fontanf May 15 '21 at 11:07
2

Besides the useful answers mentioned by community folks, some notations would be considered:

  • As there are many scheduling environments in the real situation or academic literature you should first determine which kind of scheduling model you have faced. For this, it would be helpful to see the Graham notation to determine (or at least for the benchmark) the scheduling model.

  • Please, keep in mind that in the (hybrid) flow shop or (flexible) job shop models, there is a pre-determined route for each job/task. It means that each job/task must be processed based on and there is no way to perform that on any machine or in the favorite dispatching.

As you mentioned, Any activity can be run on any machine and there is a precedence constraint for performing the jobs/tasks, it sounds like a resource-constrained project scheduling model (RCPSP). Also, to visualize the final results, there are two kinds of diagrams. First, the resource Gantt chart and the second the task Gantt chart.

I recommended you start with the RCPSP and expand it further in the next level. In the following, a variant of the mixed-integer program (time index formulation) is presented. Indeed, in contrast to the solving time, despite MIP formulation, CP is another good alternative.

\begin{split}\textrm{Minimize} & \\ & \sum_{t\in \mathcal{T}} t\cdot x_{(n+1,t)}\\ \textrm{Subject to:} & \\ \sum_{t\in \mathcal{T}} x_{(j,t)} & = 1 \,\,\, \forall j\in J\\ \sum_{j\in J} \sum_{t_2=t-p_{j}+1}^{t} u_{(j,r)}x_{(j,t_2)} & \leq c_{r} \,\,\, \forall t\in \mathcal{T}, r \in R\\ \sum_{t\in \mathcal{T}} t\cdot x_{(s,t)} - \sum_{t \in \mathcal{T}} t\cdot x_{(j,t)} & \geq p_{j} \,\,\, \forall (j,s) \in S\\ x_{(j,t)} & \in \{0,1\} \,\,\, \forall j\in J, t \in \mathcal{T}\end{split}

Where:

  • $J$ is the set of the jobs
  • $R$ is the set of the resources
  • $S$ is the precedence sets
  • $T$ is the planning duration
  • $P_{j}$ is the processing time of job $j$
  • $U_{(r,j)}$ is the amount of resource $r$ required for processing job $j$
  • $C_{r}$ is the capacity of renewable resource $r$

The resource Gantt chart of the above formulation (for $10$ tasks) is shown in the following. enter image description here

A.Omidi
  • 8,832
  • 2
  • 13
  • 49