Assignment and scheduling problem with resource constraints

Question

I have 10 tasks with 6 workers. Each worker can only serve one task at a time and must complete the task before moving on to the next task. Each worker has a maximum work output value and each task has an amount of work required. A worker can output work at any continuous value up to its maximum work output for any given minute. Each task (in units) need not begin at it's start time (in mins), but must be completed by its max_completion_time (in mins). We are trying to minimize overall workload across all workers at any given time.

Maximum work output:

Worker 1: {'max_work_output': 10 units per min, 'ramp_up': 5}
Worker 2: {'max_work_output': 10 units per min, 'ramp_up': 5}
Worker 3: {'max_work_output': 10 units per min, 'ramp_up': 5}
Worker 4: {'max_work_output': 10 units per min, 'ramp_up': 5}
Worker 5: {'max_work_output': 10 units per min, 'ramp_up': 5}
Worker 6: {'max_work_output': 50 units per min, 'ramp_up': 5}

Task work units needed, minimum start time, and maximum completion time:

Task 1:  {'work_needed': 3000 units, 'min_start_time': 0, 'max_completion_time': 600}
Task 2:  {'work_needed': 3600 units, 'min_start_time': 0, 'max_completion_time': 600}
Task 3:  {'work_needed': 1800 units, 'min_start_time': 5, 'max_completion_time': 600}
Task 4:  {'work_needed': 1200 units, 'min_start_time': 10, 'max_completion_time': 600}
Task 5:  {'work_needed': 3300 units, 'min_start_time': 15, 'max_completion_time': 600}
Task 6:  {'work_needed': 3000 units, 'min_start_time': 20, 'max_completion_time': 600}
Task 7:  {'work_needed': 3600 units, 'min_start_time': 30, 'max_completion_time': 600}
Task 8:  {'work_needed': 1800 units, 'min_start_time': 100, 'max_completion_time': 600}
Task 9:  {'work_needed': 1200 units, 'min_start_time': 100, 'max_completion_time': 600}
Task 10: {'work_needed': 3300 units, 'min_start_time': 120, 'max_completion_time': 600}

• when a worker changes it's output this can only be done at a maximum value of ramp_up. Objective: What is the optimal schedule (which includes the work output at each minute from each worker) that minimizes the maximum sum of work across each worker?

• The solution should be a 10 x 6 x 600 tensor that describes each worker's output at each minute for each task - where we minimize the sum of any matrix along the $T$ dimension

Wondering if there are any other examples of similar work or how this solution would be formalized/implemented.

Answer 1

I didn't find a way to express the transition constraints so i give a description what this does and mention what it lacks.

using JuMP
using Gurobi #needs Gurobi license but any other MILP solver callable from JuMP should work too## Heading ##
using UnicodePlots

are dependencies. I used UnicodePlots for debugging. It is neat. In Julia dependencies can be installed via ]add JuMP in the Julia shell. Gurobi also needs to be installed and have a license. Another solver like should also do the trick. Learn more here .

workers = [
  10 5;
  10 5;
  10 5;
  10 5;
  10 5;
  50 5;
]
tasks = [
  3000 1 600; #out of bounds if 0
  3600 1 600;
  1800 1 600;
  1200 10 600;
  3300 15 600;
  3000 20 600;
  3600 30 600;
  1800 100 600;
  1200 100 600;
  3300 120 600;
]
sim_time = 600; #needs to be bigger or equal than the last time stamp

Is the problem information you provided. It could have also been stored in structures, dictionaries but i went with arrays for simplicity

model = Model(Gurobi.Optimizer)
@variable(model, workspeed[1:(size(workers)[1]), 1:(size(tasks)[1]), 1:sim_time], lower_bound = 0)
for i=1:(size(workers)[1])
  @constraint(model, workspeed[i,:,:] .<= workers[i,1])
end

Since worker top speed differs there is no good way to define all upper bound at once. Here i broadcast the lesser or equal constraint over all workspeed of an particular worker.

@variable(model,p)
@constraint(model,sum(workspeed,dims=(1,2)).<=p)  #the sum over all dimensions expect time, the total work at each time point

This define the objective which is the lowest maximum over all work happening at any time point.

@variable(model, work_done[1:(size(tasks)[1]), 1:sim_time], lower_bound = 0)
for i=1:(size(tasks)[1])
  for j=1:tasks[i,2]
    @constraint(model, work_done[i,j] == 0)
  end
  for j=(tasks[i,3]):sim_time
    @constraint(model, work_done[i,j] >= tasks[i,1])
  end
end
for t=1:(sim_time-1)
  @constraint(model, work_done[:,t+1] .==  work_done[:,t] .+ sum(workspeed,dims=1)[1,:,t])
end

This block could be almost removed and i think Gurobi does that during presolve sometimes. sum([ workspeed[:,i,t] for t=(tasks[i,2]):(tasks[i,3])]) >= tasks[i,1] or something similar could do the trick and eliminate the necessity for work_done completely. This block makes sure that work on tasks is not started early or finishes late.

for t=1:(sim_time-1)
  for w=1:(size(workers)[1])
    @constraint(model, -workers[w,2] .<= workspeed[w,:,t+1] .- workspeed[w,:,t] .<= workers[w,2] ) # different ramp down?
  end
end

constrains the growth/decline of the all individual workspeeds. In the previous version i had constrained the sum instead which allowed the solver to keep production speed when switching tasks. Now that this constraint is enforced properly, switching can still happen for free and instantly when production speed is <= the wind_up without down time.

@variable(model, workson[1:(size(workers)[1]), 1:(size(tasks)[1]), 1:sim_time], Bin)
@variable(model, worksonatall[1:(size(workers)[1]), 1:(size(tasks)[1])], Bin)

These binary variables are responsible for enforcing the scheduling logic. If a worker n ever works task t value(worksonatall[n,t]) will be true. While forcing certain values to false can be used to forbid people from working on something, it would be more smart to not generate the backbone in workspeed and other places. While presolve might remove it would be better not to generate it at all.

Note that without this logic a linear program would result which could be solved a lot faster.

for i=1:(size(workers)[1])
  @constraint(model, workspeed[i,:,:] .<= workers[i,1] * workson[i,:,:] )
end

This ensures that if a worker works on some task at some time that this information is available as a boolean.

@constraint(model, sim_time*worksonatall[:,:] .>= sum(workson,dims=3)[:,:,1]) # any
@constraint(model, sum(workson,dims=3)[:,:,1] .>= worksonatall[:,:]) # any

This code established the relationship between workson and worksonatall the latter is the logical or over all time of workson.

@constraint(model, sum(worksonatall, dims=1)[1,:] .== 1)

Every task can only ever be worked on by one worker.

for t=1:sim_time
      for w=1:(size(workers)[1])
      @constraint(model,sum(workson[w,:,t]) <= 1)
    end
end

A worker can work at most at one task at a time.

@objective(model, Min, p)
optimize!(model)
println(value.(worksonatall))

Defines objective and hands problem to the solver. Show which worker work on what which is useful for debugging.

I let the program run over night on my quadcore. Gurobi found an global optimum. The resulting array of workspeed is pasted here. Here is an excerpt of the log for every time a new incumbent integer solution was found:

    Nodes    |    Current Node    |     Objective Bounds      |     Work
 Expl Unexpl |  Obj  Depth IntInf | Incumbent    BestBd   Gap | It/Node Time

2465  1985             731      43.7307033   43.07179  1.51%   421 1356s

H 2649   930                      43.4719711   43.07179  0.92%   402 1884s
H 2877   601                      43.2761578   43.07179  0.47%   422 1983s
H 2879   571                      43.2646048   43.07179  0.45%   422 2321s
H 2879   543                      43.2423208   43.07179  0.39%   422 2321s
H 2880   516                      43.2367973   43.07179  0.38%   422 2762s
H 2888   495                      43.2312925   43.07179  0.37%   421 6594s
H 2956   566                      43.2282794   43.07179  0.36%  1065 13263s
H 2978   535                      43.2033898   43.07179  0.30%  1141 13263s
H 3006   683                      43.1895093   43.07179  0.27%  1165 15293s
H 3340  1119                      43.1725888   43.07179  0.23%  1567 16752s
H 3489  1048                      43.1587838   43.07179  0.20%  1591 16752s
H 4936  1195                      43.1418919   43.07179  0.16%  1459 18634s
H 4963  1148                      43.1165541   43.07179  0.10%  1461 19244s
H 9711   972                      43.1008403   43.07179  0.07%  1470 27005s
H11482   430                      43.0904523   43.07179  0.04%  1498 29415s
H12431   220                      43.0717863   43.07179  0.00%  1513 31324s

The resulting objective is 43.071786310517524.

workspeed by workers over time

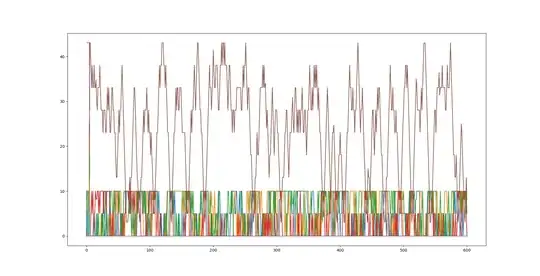
workspeed on tasks over time 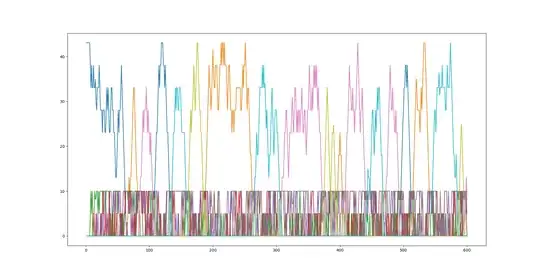We see that the tasks in the current formulation can get resumed later. The easiest way to achieve no resumes would be to constrain the sum of xors between successive workson to be 2 and to set initial workspeed to 0 for all workers, alternatively or with some amount related to the sum of workson could work to. At the moment worker 6 starts with the maximal work speed. This would almost double the amount of binary values though and make the search space less relaxed. See here how to do or and xor. However i think there should be a better solution.

work_done on tasks over time

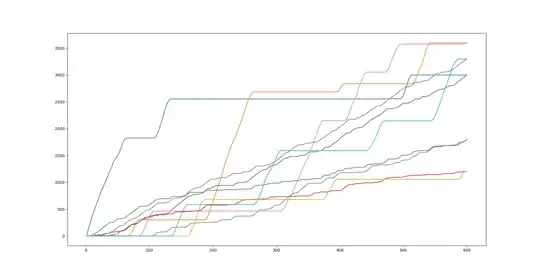
sum of workspeed over time